题目内容
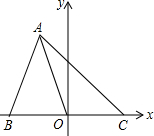 (2014•静安区一模)如图,已知在直角坐标系中,点A在第二象限内,点B和点C在x轴上,原点O为边BC的中点,BC=4,AO=AB,tan∠AOB=3,求图象经过A、B、C三点的二次函数解析式.
(2014•静安区一模)如图,已知在直角坐标系中,点A在第二象限内,点B和点C在x轴上,原点O为边BC的中点,BC=4,AO=AB,tan∠AOB=3,求图象经过A、B、C三点的二次函数解析式.分析:先确定B点坐标为(-2,0),C点坐标为(2,0),作AH⊥OB于H,根据等腰三角形的性质得到OH=BH=1,再利用三角形函数得到tan∠AOB=
=3,则AH=3,所以A点坐标为(-1,3),设抛物线的交点式y=a(x+2)(x-2),然后把A点坐标代入求出a即可.
| AH |
| OH |
解答: 解:∵原点O为边BC的中点,BC=4,
解:∵原点O为边BC的中点,BC=4,
∴B点坐标为(-2,0),C点坐标为(2,0),
作AH⊥OB于H,如图,
∵AO=AB,
∴OH=BH=1,
∵tan∠AOB=
=3,
∴AH=3,
∴A点坐标为(-1,3),
设抛物线的解析式为y=a(x+2)(x-2),
把A(-1,3)代入得a×1×(-3)=3,
解得a=-1,
∴经过A、B、C三点的二次函数解析式为y=-(x+2)(x-2)=-x2+4.
 解:∵原点O为边BC的中点,BC=4,
解:∵原点O为边BC的中点,BC=4,∴B点坐标为(-2,0),C点坐标为(2,0),
作AH⊥OB于H,如图,
∵AO=AB,
∴OH=BH=1,
∵tan∠AOB=
| AH |
| OH |
∴AH=3,
∴A点坐标为(-1,3),
设抛物线的解析式为y=a(x+2)(x-2),
把A(-1,3)代入得a×1×(-3)=3,
解得a=-1,
∴经过A、B、C三点的二次函数解析式为y=-(x+2)(x-2)=-x2+4.
点评:本题考查了待定系数法求二次函数关系式:要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 (2014•静安区一模)如图,已知平行四边形ABCD中,向量
(2014•静安区一模)如图,已知平行四边形ABCD中,向量 (2014•静安区一模)如图,已知AB、CD分别表示两幢相距30米的大楼,小明在大楼底部点B处观察,当仰角增大到30度时,恰好能通过大楼CD的玻璃幕墙看到大楼AB的顶部点A的像,那么大楼AB的高度为( )
(2014•静安区一模)如图,已知AB、CD分别表示两幢相距30米的大楼,小明在大楼底部点B处观察,当仰角增大到30度时,恰好能通过大楼CD的玻璃幕墙看到大楼AB的顶部点A的像,那么大楼AB的高度为( )