Question

已知：0＜a＜b＜c，实数x、y满足2x+2y=a+b+c，2xy=ac，且x＜y．求证：0＜x＜a，b＜y＜c．

Answer 1

证明：∵2x+2y=a+b+c，2xy=ac，
∴x+y=

a+b+c

2

，xy=

ac

2

，
∴x，y可看作方程t²-

a+b+c

2

t+

ac

2

=0的两实根，
设函数S=t²-

1

2

（a+b+c）t+

1

2

ac，
①当t=0时，S=

1

2

ac＞0；
②当t=a时，S=a²-

a+b+c

2

•a+

ac

2

=

1

2

a（a-b），
而0＜a＜b，
∴S=

1

2

a（a-b）＜0；
③当t=b时，S=b²-

1

2

（a+b+c）b+

1

2

ac=

1

2

（b-a）（b-c），
∵0＜a＜b＜c，
∴S=

1

2

（b-a）（b-c）＜0，
④当t=c时，S=

1

2

c（c-b）＞0，
可知函数S=t²-

1

2

（a+b+c）t+

1

2

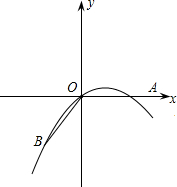
ac的图象与t轴的两个交点分别在0，a和b，c之间，如图，
∴方程t²-

a+b+c

2

t+

ac

2

=0的两根分别在0，a之间的和b，c之间，
即0＜x＜a，b＜y＜c．