题目内容
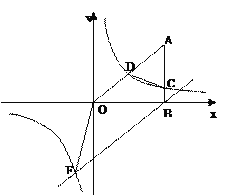
【题目】(本题8分)如图, ![]() 轴于点
轴于点![]() ,
,  ,反比例函数
,反比例函数![]() 与OA、AB分别相交于点D、C,且点D为OA的中点.
与OA、AB分别相交于点D、C,且点D为OA的中点.
(1)求反比例函数的解析式;
(2)过点B的直线![]() 与反比例函数
与反比例函数![]() 图象交于第三象限内一点F,求四边形
图象交于第三象限内一点F,求四边形![]() 的面积.
的面积.
【答案】![]()
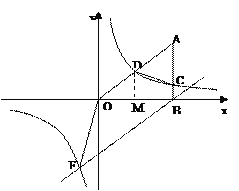
解:过D作DM⊥x轴交OB于点M。
∵AB⊥x轴于B, ∴∠DMO=∠ABO=90°∴DM∥AB,
∴![]() ,而D为OA中点,
,而D为OA中点, ![]()
DM=![]() ,又∵
,又∵![]() ,
,![]()
∴OB=8,AB=6,∴OM=4,DM=3
∴![]() =3×4=12
=3×4=12
∴反比例函数的解析式为: ![]()
(2)将![]() 代入
代入![]() 得
得![]() ,联立
,联立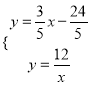
得![]() ,∴F(-2,-6),∴
,∴F(-2,-6),∴![]() =
=![]() =
=![]() =48.
=48.

【解析】试题解析:试题分析:(1)过点D作DM⊥x轴,通过正弦函数得出AB的长,即可得出A的坐标,进而得出D的坐标,代入 ![]() ,根据待定系数法即可求得;
,根据待定系数法即可求得;
(2)易求得直线BF的解析式,然后联立方程求得F的坐标,过点F作FN⊥x轴,
根据S四边形OFBA=S△AOB+S△BOF求得即可.
解:过D作DM⊥x轴交OB于点M。
∵AB⊥x轴于B, ∴∠DMO=∠ABO=90°∴DM∥AB,
∴![]() ,而D为OA中点,
,而D为OA中点, ![]()
DM=![]() ,又∵
,又∵![]() ,
,![]()
∴OB=8,AB=6,∴OM=4,DM=3
∴![]() =3×4=12
=3×4=12
∴反比例函数的解析式为: ![]()
(2)将![]() 代入
代入![]() 得
得![]() ,联立
,联立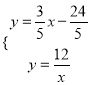
得![]() ,∴F(-2,-6),∴
,∴F(-2,-6),∴![]() =
=![]() =
=![]() =48.
=48.

练习册系列答案
相关题目




