题目内容
【题目】(本小题满分12分)在△ABC中,AB=AC,P是BC上任意一点.
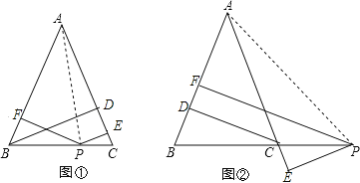
(1)如图①,若P是BC边上任意一点,PF⊥AB于点F,PE⊥AC于点E,BD为△ABC的高线,试探求PE,PF与BD之间的数量关系;

(2)如图②,若P是BC延长线上一点,PF⊥AB于点F,PE⊥AC于点E,CD为△ABC的高线,试探求PE,PF与CD之间的数量关系.

【答案】(1)BD=PE+PF;
(2)CD=PF﹣PE.
【解析】
试题分析:(1)连接AP,根据S△ABC=S△ABP+S△ACP列式整理即可得解;
(2)连接AP,根据S△ABC=S△ABP﹣S△ACP列式整理即可得解.
试题解析:(1)如图,连接AP,则S△ABC=S△ABP+S△ACP,
所以,![]() ACBD=
ACBD=![]() ABPF+
ABPF+![]() ACPE,
ACPE,
∵AB=AC,
∴BD=PE+PF;
(2)连接AP,则S△ABC=S△ABP﹣S△ACP,
所以,![]() ABCD=
ABCD=![]() ABPF﹣
ABPF﹣![]() ACPE,
ACPE,
∵AB=AC,
∴CD=PF﹣PE.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目