题目内容
【题目】二次函数y=ax2+bx+c的部分图象如图所示,则下列正确的说法有( )
①点P(ac,b)在第二象限;
②x>1时y随x的增大而增大;
③b2﹣4ac>0;
④关于x的一元二次方程ax2+bx+c=0解为x1=﹣1,x2=3;
⑤关于x的不等式ax2+bx+c>0 的解集为0<x<3.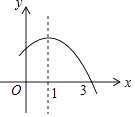
A.2个
B.3个
C.4个
D.5个
【答案】B
【解析】解:①∵抛物线的开口向下,
∴a<0,
∵抛物线的对称轴在y轴的右侧,即x=﹣ ![]() >0,
>0,
∴b>0,
由图象可知抛物线与y轴的交点(0,c)在y轴的正半轴,
∴c>0,
∴ac<0
∴点P(ac,b)在第二象限;
所以此选项说法正确;
②由图象得:当x>1时,y随x的增大而减小;
所以此选项说法不正确;
③∵抛物线与x轴有2个交点,
∴b2﹣4ac>0,
所以此选项说法正确;
④由图象得:抛物线的对称轴是:x=1,
由对称性得:抛物线与x轴的交点是(﹣1,0)、(3,0),
∴关于x的一元二次方程ax2+bx+c=0解为x1=﹣1,x2=3;
所以此选项说法正确;
⑤由图象得:当﹣1<x<3时,y>0,
∴关于x的不等式ax2+bx+c>0 的解集为﹣1<x<3,
所以此选项说法不正确;
所以本题说法正确的有:3个,
故选:B.
【考点精析】本题主要考查了二次函数图象以及系数a、b、c的关系和抛物线与坐标轴的交点的相关知识点,需要掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c);一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能正确解答此题.

【题目】某学校对学生的课外阅读时间进行抽样调查,将收集的数据分成A、B、C、D、E五组进行整理,并绘制成如下的统计图表(图中信息不完整).
组别 | 阅读时间x(时) | 人数 |
A | 0≤x<10 | k |
B | 10≤x<20 | 100 |
C | 20≤x<30 | m |
D | 30≤x<40 | 140 |
E | x≥40 | n |

请结合以上信息解答下列问题
(1)阅读时间分组统计表中k、m、n的值分别是 、 、 ;
(2)补全“阅读人数分组统计图”;
(3)若全校有3000名学生,请估算全校课外阅读时间在20小时以下(不含20小时)的




