Question

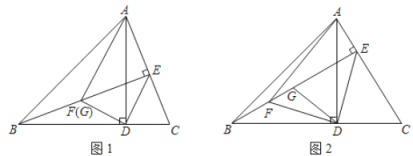
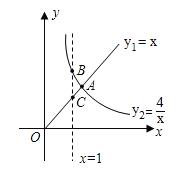
【题目】如图（1）,在Rt△ABC,∠ACB=90°,分别以AB、BC为一边向外作正方形ABFG、BCED,连结AD、CF,AD与CF交于点M；

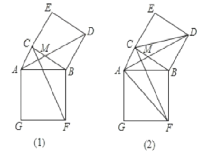
(1)求证:△ABD≌△FBC；

(2) 如图(2)，已知AD=6，求四边形AFDC的面积；

Answer 1

【答案】（1）见解析；（2）18.

【解析】

（1）根据四边形ABFG、BCED是正方形得到两对边相等，一对直角相等，根据图形利用等式的性质得到一对角相等，利用SAS即可得到三角形全等；

（2）连接FD，由（1）的三角形全等，得到AD=FC，∠BAD=∠BFC，利用等式的性质及垂直定义得到AD与CF垂直，四边形AFDC面积=三角形ACD面积+三角形ACF面积+三角形DMF面积-三角形ACM面积，求出即可；

(1)∵四边形ABFG、BCED是正方形，

∴AB=FB,CB=DB,∠ABF=∠CBD=90°，

∴∠ABF+∠ABC=∠CBD+∠ABC，

即∠ABD=∠CBF，

在△ABD和△FBC中，

，

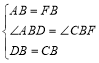∴△ABD≌△FBC(SAS)；

(2)连接FD，设CF与AB交于点N，

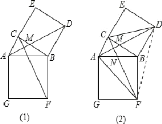
∵△ABD≌△FBC，

∴AD=FC，∠BAD=∠BFC，

∴∠AMF=180°∠BAD∠CNA=180°(∠BFC+∠BNF)=180°90°=90°，

∴AD⊥CF，

∵AD=6，

∴FC=AD=6，

∴S =S +S +S S ,

=ADCM+CFAM+DMFMAMCM,

=3CM+3AM+ (6AM)(6CM) AMCM=18；