题目内容
【题目】在平面直角坐标系中,直线y=k1x+b与x轴交于点B,与y轴交于点C,与反比例函数y=
的图象在第一象限交于点A（3,1），连接OA．
（1）求反比例函数y=
的解析式；
（2）若S△AOB：S△BOC=1：2，求直线y=k1x+b的解析式．
【答案】（1）反比例函数的解析式为y=
；（2）直线的解析式为y=x﹣2；（3）直线的解析式为y=﹣
x+2.
【解析】（1）将点A的坐标代入反比例函数解析式中，得出关于k2的一元一次方程，解方程即可得出结论；
（2）分两种情况考虑：①直线y=k1x+b经过第一、三、四象限，由S△AOB：S△BOC=1：2结合三角形的面积公式得出C的坐标，由待定系数法即可求出此时直线的函数解析式；②直线y=k1x+b经过第一、二、四象限，由S△AOB：S△BOC=1：2结合三角形的面积公式得出点C的坐标，由待定系数法即可求出此时直线的函数解析式.
解：（1）将点A（3，1）代入到y=
中，得1=
，解得：k2=3．
故反比例函数的解析式为y=
．
（2）符合题意有两种情况：①直线y=k1x+b经过第一、三、四象限，如图1所示．
∵S△AOB：S△BOC=1：2，点A（3，1），∴点C的坐标为（0，﹣2）．
则有
，解得：
．
∴直线的解析式为y=x﹣2．
②直线y=k1x+b经过第一、二、四象限，如图2所示．
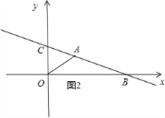
∵S△AOB：S△BOC=1：2，点A（3，1），∴点C的坐标为（0，2）．
则有
，解得：
．
∴直线的解析式为y=﹣
x+2．
“点睛”本题考查了反比例函数与一次函数交点的问题、待定系数法求函数解析式以及三角形的面积公式，解题的关键：（1）将点A的坐标代入反比例函数解析式中得到关于k2的一元一次方程；（2）分两种情况分别求出点C的坐标.本题属于基础题，难度不大，解决该题型题目时，结合点的坐标利用待定系数法求出函数解析式是关键.
