题目内容
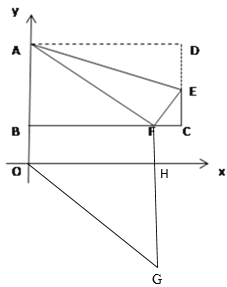
【题目】已知矩形ABCD,AB=6,BC=10,以BC所在直线为x轴,AB所在直线为y轴,建立如图所示的平面直角坐标系,在CD边上取一点E,将△ADE沿AE翻折,点D恰好落在BC边上的点F处.
(1)求线段EF长;
(2)在平面内找一点G,
①使得以A、B、F、G为顶点的四边形是平行四边形,请直接写出点G的坐标;
②如图2,将图1翻折后的矩形沿y轴正半轴向上平移m个单位,若四边形AOGF为菱形,请求出m的值并写出点G的坐标.

【答案】(1)EF=![]() ;(2)①点G的坐标为(-8,6)或(8,6)或(8,-6);②m=4,点G的坐标是(8,-6).
;(2)①点G的坐标为(-8,6)或(8,6)或(8,-6);②m=4,点G的坐标是(8,-6).
【解析】
(1)由矩形的性质得到AD=BC=10,CD=AB=6,由折叠得AF=AD=10,根据勾股定理求出OF=8,得到FC=OC-OF=2,再利用勾股定理得到![]() ,即可求出EF;
,即可求出EF;
(2)①分别以AB、AF、BF为平行四边形的对角线,根据平行四边形的性质得到点G的坐标;
②根据菱形的性质求出AO=AF=10,由此得到平移的距离m=4, 设FG交x轴于点H,证明四边形OBFH是矩形,得到=OB=4,OH=BF=8,求出HG=10-4=6,由此求出点G的坐标是(8,-6).
(1)∵四边形ABCD是矩形,
∴AD=BC=10,CD=AB=6,
由折叠得AF=AD=10,
∵∠AOC=90°,AO=6,
∴OF=8,
∴FC=OC-OF=2,
在Rt△EFC中,![]() ,
,
∴![]() ,
,
解得EF=![]() ;
;
(2)①当AB为平行四边形的对角线时,AG=BF且AG∥BF,∴点G的坐标为(-8,6);
当AF为平行四边形的对角线时,AG=BF且AG∥BF,∴点G的坐标为(8,6);
当BF为平行四边形的对角线时,FG=AB且FG∥AB,∴点G的坐标为(8,-6);
综上,点G的坐标为(-8,6)或(8,6)或(8,-6);
②∵四边形AOGF是菱形,
∴AO=AF=10,
∴矩形ABCD平移的距离m=AO-AB=10-6=4,即OB=4,
设FG交x轴于点H,
∵AO∥FG,BC∥x轴,
∴∠FBO=∠BOH=∠OHF=90°,
∴四边形OBFH是矩形,
∴FH=OB=4,OH=BF=8,
∴HG=10-4=6,
∴点G的坐标是(8,-6).