题目内容
(2012•高新区一模)下面是李刚同学在一次测验中解答的数学题:
①若x2=4,则x=2,
②方程x(x-1)=2(x-1)的解为x=2,
③若x2+2x+k=0两根的倒数和等于4,则k=-
,
④若x=0是方程(m-2)x2+3x+m2+2m-8=0的解,则m=2或-4.
其中答对的是
①若x2=4,则x=2,
②方程x(x-1)=2(x-1)的解为x=2,
③若x2+2x+k=0两根的倒数和等于4,则k=-
| 1 | 2 |
④若x=0是方程(m-2)x2+3x+m2+2m-8=0的解,则m=2或-4.
其中答对的是
③④
③④
(填序号)分析:①直接开方即可;
②原方程可化为:(x-2)(x-1)=0,那么它的解就是x=2或x=1;
③根据题意可得
+
=4,左边通分可得
=4,再根据根与系数的关系,可知x1+x2=-2,x1x2=k,再代入可得
=4,解可求k的值;
④把x=0代入方程,可得m2+2m-8=0,解可求m=2或m=-4.
②原方程可化为:(x-2)(x-1)=0,那么它的解就是x=2或x=1;
③根据题意可得
| 1 |
| x1 |
| 1 |
| x2 |
| x1x2 |
| x1x2 |
| -2 |
| k |
④把x=0代入方程,可得m2+2m-8=0,解可求m=2或m=-4.
解答:解:①若x2=4,则x=±2,故此选项错误;
②方程x(x-1)=2(x-1),的解为x=2或x=1,故此选项错误;
③若x2+2x+k=0两根的倒数和等于4,
∴x1+x2=-2,x1x2=k,
∴
+
=
=-
=4
解得k=-
,此选项正确;
④若x=0是方程(m-2)x2+3x+m2+2m-8=0的解,则m=2或-4,此选项正确.
故答案是③④.
②方程x(x-1)=2(x-1),的解为x=2或x=1,故此选项错误;
③若x2+2x+k=0两根的倒数和等于4,
∴x1+x2=-2,x1x2=k,
∴
| 1 |
| x1 |
| 1 |
| x2 |
| x1+x2 |
| x1x2 |
| 2 |
| k |
解得k=-
| 1 |
| 2 |
④若x=0是方程(m-2)x2+3x+m2+2m-8=0的解,则m=2或-4,此选项正确.
故答案是③④.
点评:本题考查了一元二次方程的解、解一元二次方程,解题的关键是注意不要漏解.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
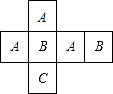 (2012•高新区一模)一个材质均匀的正方体的六个面上分别标有字母A、B、C,其展开图如图所示,随机抛掷此正方体,A面朝上的概率是
(2012•高新区一模)一个材质均匀的正方体的六个面上分别标有字母A、B、C,其展开图如图所示,随机抛掷此正方体,A面朝上的概率是