题目内容
已知:如图,在△ABC中,∠BAC=120°,AB=AC,BC=4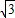 ,以A为圆心,2为半径作⊙A,试问:直线BC与⊙A的关系如何?并证明你的结论.
,以A为圆心,2为半径作⊙A,试问:直线BC与⊙A的关系如何?并证明你的结论.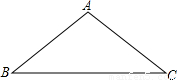
【答案】分析:作AD⊥BC垂足为D,根据已知,利用勾股定理求得AD的长,将AD的长与半径2作比较;进而由(当AD>2时,相交;当AD=2时,相切;当AD<2时,相离),从而确定直线BC与⊙A的关系.
解答: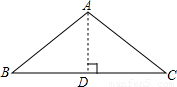 解:作AD⊥BC垂足为D;
解:作AD⊥BC垂足为D;
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°;
∵BC=4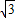 ,
,
∴BD= BC=2
BC=2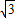 ,
,
可得AD=2;
又∵⊙A半径为2,
∴⊙A与BC相切.
点评:此题主要考查了直线与圆的位置关系:若直线到圆心的距离为d,圆的半径为r,当d>r时,相离;当d=r时,相切;当d<r时,相交.
解答:
 解:作AD⊥BC垂足为D;
解:作AD⊥BC垂足为D;∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°;
∵BC=4
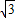 ,
,∴BD=
 BC=2
BC=2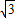 ,
,可得AD=2;
又∵⊙A半径为2,
∴⊙A与BC相切.
点评:此题主要考查了直线与圆的位置关系:若直线到圆心的距离为d,圆的半径为r,当d>r时,相离;当d=r时,相切;当d<r时,相交.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
 34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2, (2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.
(2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D. 已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E.
已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E. 已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,