题目内容
【题目】如图,矩形ABCD中,P为AD上一点,将△ABP沿BP翻折至△EBP,点A与点E重合;
(1)如图1,若AB=10,BC=6,点E落在CD边上,求AP的长;
(2)如图2,若AB=8,BC=6, PE与CD相交于点O,且OE=OD,求AP的长;
(3)如图3,若AB=4,BC=6,点P是AD的中点,求DE的长.

【答案】(1)![]() (2)4.8(3)3.6
(2)4.8(3)3.6
【解析】试题分析:(1)在Rt△BCE中,BC=6,BE=AB=10,根据勾股定理求出CE的值为8,则DE=10-8=2,设AP=x,则PE=x,DP=6-x,在Rt△DPE中,根据勾股定理得出方程,解方程即可;
(2)由折叠的性质得出EP=AP,∠E=∠A=90°,BE=AB=8,由ASA证明△ODP≌△OEG,得出OP=OG,PD=GE,设AP=EP=x,则PD=GE=6-x,DG=x,求出CG、BG,根据勾股定理得出方程,解方程即可;
(3)以点A为原点建立平面直角坐标系,则点A(0,0),B(4,0),C(4,6),D(0,6),P(0,3),设点E的坐标为(x,y),根据PE=PA=3可得,PE=![]() ,BE=
,BE=![]() ,解得y=
,解得y= ![]() ,再将y=
,再将y= ![]() 代入
代入![]() 中得,x(
中得,x(![]() )=0,所以x=0或x=
)=0,所以x=0或x=![]() ,所以y=
,所以y=![]() ,再根据DE=
,再根据DE=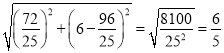 ;
;
试题解析:
(1)∵△ABP沿BP翻折至△EBP,点A与点E重合,AB=10,
∴BE=AB=10,PE=AP,
∴在Rt△BCE中,CE=![]() ,
,
∴DE=CD-CE=2,
设AP=x,则DP=6-x
∵在Rt△DPE中,DP2+DE2=PE2,
∴(6-x)2+22=x2,
∴x=![]() ;
;
(2)∵四边形ABCD是矩形,
∴∠D=∠A=∠C=90°,AD=BC=6,CD=AB=8,
根据题意得:△ABP≌△EBP,
∴EP=AP,∠E=∠A=90°,BE=AB=8,
在△ODP和△OEG中,
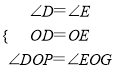
∴△ODP≌△OEG(ASA),
∴OP=OG,PD=GE,
∴DG=EP,
设AP=EP=x,则PD=GE=6-x,DG=x,
∴CG=8-x,BG=8-(6-x)=2+x,
根据勾股定理得:BC2+CG2=BG2,
即62+(8-x)2=(x+2)2,
解得:x=4.8,
∴AP=4.8;
(3)以点A为原点建立平面直角坐标系,则点A(0,0),B(4,0),C(4,6),D(0,6),P(0,3),设点E的坐标为(x,y),根据PE=PA=3可得,
PE=![]() ,BE=
,BE=![]() ,
,
解得y= ![]() ,
,
把y= ![]() 代入
代入![]() 中得,
中得,
x(![]() )=0,
)=0,
所以x=0(舍去)或x=![]() ,
,
所以y=![]() ,
,
∴DE=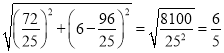 ;
;

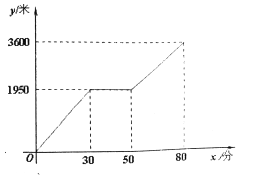
【题目】学校国旗护卫队成员的身高分布加下表:
身高/cm | 159 | 160 | 161 | 162 |
人数 | 7 | 10 | 9 | 9 |
则学校国旗护卫队成员的身高的众数和中位数分别是( )
A.160和160B.160和160.5C.160和161D.161和161
【题目】九年级一班数学老师对全班学生在模拟考试中A卷成绩进行统计后,制成如下的统计表:
成绩(分) | 80 | 82 | 84 | 86 | 87 | 90 |
人数 | 8 | 12 | 9 | 3 | 5 | 8 |
则该班学生A卷成绩的众数和中位数分别是( )
A. 82分,82分 B. 82分,83分 C. 80分,82分 D. 82分,84分