题目内容
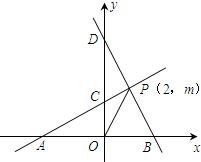 已知,如图1所示,直线PA与x轴交于点A,与y轴交于点C(0,2),且S△AOC=4,直线BD与x轴交于点B,与y轴交于点D,直线PA与直线BD交于点P(2,m),点P在第一象限,连接OP.
已知,如图1所示,直线PA与x轴交于点A,与y轴交于点C(0,2),且S△AOC=4,直线BD与x轴交于点B,与y轴交于点D,直线PA与直线BD交于点P(2,m),点P在第一象限,连接OP.
(1)求点A的坐标;
(2)求直线PA的函数表达式;
(3)求m的值;
(4)若S△BOP=S△DOP,请你直接写出直线BD的函数表达式.
解:(1)∵点C(0,2),S△AOC=4,
而S△AOC= AO•OC,
AO•OC,
∴AO=4,
∴点A的坐标为(-4,0);
(2)设直线PA的解析式为y=kx+b,
则有 ,
,
解之得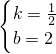 ,
,
∴直线PA的解析式为y= x+2;
x+2;
(3)∵点P(2,m)在直线PA上,
∴m= ×2+2,
×2+2,
∴m=3;
(4)解:∵S△BOP=S△DOP,△BOP的边BP上的高和△DOP的边DP上的高相同,
∴PD=PB,
即P为BD中点,
过P作PM⊥OB于M,PN⊥OD于N,
则PM∥OD,PN∥OB,
∴OM=BM,ON=DN,
∴OD=2PM,OB=2PN,
∵P(2,3),
∴PM=3,PN=2,
∴OD=6,OB=4,
即D(0,6),B(4,0),
设直线BD的解析式是y=kx+b,
则 ,
,
解得:k=- ,b=6,
,b=6,
∴直线BD的解析式为y=- x+6.
x+6.
分析:(1)由于点C(0,2),且S△AOC=4,利用三角形的面积公式可以求出AO的长度,然后就可以求出点A的坐标;
(2)由于直线PA经过A、C,利用待定系数法即可确定直线PA的函数表达式;
(3)由于直线PA与直线BD交于点P(2,m),直接把P(2,m)代入直线PA的解析式中即可求出m的值;
(4)由于S△BOP=S△DOP,由此得到P是BD的中点,由此可以确定D的坐标,然后就可以确定直线BD的函数表达式.
点评:此题主要考查了一次函数的图象和性质,也考查了三角形的面积公式及待定系数法确定函数的解析式,解题时首先利用三角形的面积公式确定点的坐标,然后利用待定系数法确定函数的解析式即可解决问题.
而S△AOC=
 AO•OC,
AO•OC,∴AO=4,
∴点A的坐标为(-4,0);
(2)设直线PA的解析式为y=kx+b,
则有
 ,
,解之得
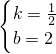 ,
,∴直线PA的解析式为y=
 x+2;
x+2;(3)∵点P(2,m)在直线PA上,
∴m=
 ×2+2,
×2+2,∴m=3;
(4)解:∵S△BOP=S△DOP,△BOP的边BP上的高和△DOP的边DP上的高相同,
∴PD=PB,
即P为BD中点,

过P作PM⊥OB于M,PN⊥OD于N,
则PM∥OD,PN∥OB,
∴OM=BM,ON=DN,
∴OD=2PM,OB=2PN,
∵P(2,3),
∴PM=3,PN=2,
∴OD=6,OB=4,
即D(0,6),B(4,0),
设直线BD的解析式是y=kx+b,
则
 ,
,解得:k=-
 ,b=6,
,b=6,∴直线BD的解析式为y=-
 x+6.
x+6.分析:(1)由于点C(0,2),且S△AOC=4,利用三角形的面积公式可以求出AO的长度,然后就可以求出点A的坐标;
(2)由于直线PA经过A、C,利用待定系数法即可确定直线PA的函数表达式;
(3)由于直线PA与直线BD交于点P(2,m),直接把P(2,m)代入直线PA的解析式中即可求出m的值;
(4)由于S△BOP=S△DOP,由此得到P是BD的中点,由此可以确定D的坐标,然后就可以确定直线BD的函数表达式.
点评:此题主要考查了一次函数的图象和性质,也考查了三角形的面积公式及待定系数法确定函数的解析式,解题时首先利用三角形的面积公式确定点的坐标,然后利用待定系数法确定函数的解析式即可解决问题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
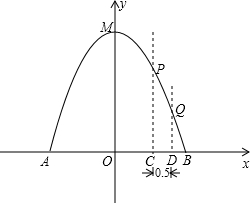 的体积和圆柱形桶的厚度忽略不计),以M点为顶点,抛物线对称轴为y轴,水平地面为x轴建立平面直角坐标系.
的体积和圆柱形桶的厚度忽略不计),以M点为顶点,抛物线对称轴为y轴,水平地面为x轴建立平面直角坐标系. 19、如图所示,在直角坐标系中,矩形OBCD的边长OB=4,OD=2.
19、如图所示,在直角坐标系中,矩形OBCD的边长OB=4,OD=2.