Question

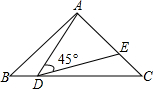在Rt△ABC中，∠BAC=90°，AB=AC=10，点D在BC所在的直线上运动，作∠ADE=45°（A，D，E按逆时针方向）．如图，若点D在线段BC上运动，DE交AC于E．
（1）求证：△ABD∽△DCE；
（2）若点D的运动速度为1个单位长度每秒时，设y=AD²，点D的运动时间为t，求y与t的函数关系，并求当△ADE是等腰三角形时AE的长．

Answer 1

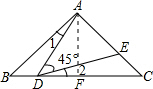解：（1）如图，∵∠BAC=90°，AB=AC，
∴∠B=∠C=45°．
又∵∠2+∠ADE=∠1+∠B，即∠2+45°=∠1+45°，
∴∠1=∠2，
∴△ABD∽△DCE；

（2）如图，过点A作AF⊥BC于点F．
易求AF=BF=5，则AD²=DF²+AF²．
所以，根据题意，得到：
y=（5-t）²+50，即y=t²-10t+100（0≤t≤10）．
当△ADE是等腰三角形时，分三种情况：
①当AD=AE时，∠ADE=∠AED=45°时，得到∠DAE=90°，点D、E分别与B、C重合，则AE=AC=10．
②当AD=DE时，由①知△ABD∽△DCE，
又∵AD=DE，知△ABD≌△DCE．
∴AB=CD=10，∴BD=CE=10-10，
∴AE=AC-CE=20-10．
③当AE=DE时，有∠EAD=∠ADE=45°=∠C，
故∠ADC=∠AED=90°．
∴DE=AE=AC=5．
综上所述，当AE的长度为10、20-10、5时，△ADE是等腰三角形．
分析：（1）根据等腰直角三角形的性质得到∠B=∠C=45°；由三角形外角的性质得到∠2+∠ADE=∠1+∠B，即∠2+45°=∠1+45°，故∠1=∠2；所以由“两角法”判定这两个三角形相似；
（2）如图，过点A作AF⊥BC于点F．根据等腰直角三角形的性质易求AF=BF=5，则AD²=DF²+AF²．把相关线段的长度代入即可求得y与t的函数关系式；当△ADE是等腰三角形时，需要分AD=AE、AD=DE、AE=DE三种情况进行讨论．
点评：考查相似三角形的判定和性质，相似三角形和全等三角形的转化．分情况讨论等腰三角形的可能性．