题目内容
【题目】在四边形ABCD中，
，对角线AC平分
．
如图1，若
，
，探究AD、AB与对角线AC三者之间的数量关系，写出结论，不必证明．
如图2若将中的条件“”去掉，中的结论是否还成立？并证明你的结论；
如图3，若
，试探究AD、AB与对角线AC三者之间的数量关系，写出结论，不必证明．
【答案】（1）
；（2）成立；（3）
.
【解析】
结论：
，只要证明
，
即可解决问题；
中的结论成立
以C为顶点，AC为一边作
，
的另一边交AB延长线于点E，只要证明
≌
即可解决问题；
结论：
过点C作
交AB的延长线于点E，只要证明
是等腰直角三角形，≌即可解决问题；
解：
．
理由如下：如图1中，
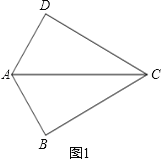
在四边形ABCD中，
，
，
，
，AC平分
，
，
，
，同理
．
．
中的结论成立，理由如下：以C为顶点，AC为一边作
，
的另一边交AB延长线于点E，
，
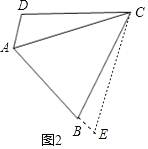
为等边三角形，
，
，
，
，
，
，
，
，
，
≌
，
，
．
结论：
理由如下：
过点C作
交AB的延长线于点E，
，
，
，
，
，
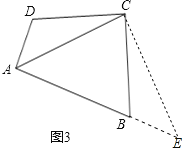
又
平分，
，
．
．
又，
，
≌
，
，
．
在
中，
，
，
．
练习册系列答案
全能闯关100分系列答案
相关题目
