��Ŀ����
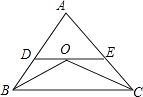
����Ŀ����ͼ1,ֱ��AB�ֱ���x�ᡢy�ύ��A��B����,OCƽ�֡�AOB��AB�ڵ�C,��DΪ�߶�AB��һ��,����D��DE//OC��y���ڵ�E,��֪AO=m,BO=n,��m��n����n2-12+36+|n-2m|=0.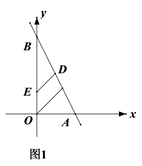
��1����A��B���������?
��2������DΪAB�е�,��OE�ij�?
��3����ͼ2,����P(x,-2x+6)Ϊֱ��AB��x���·���һ��,��E��y�����������һ����,��EΪֱ�Ƕ���������ֱ�ǡ�PEF,ʹ��F�ڵ�һ����,��F��ĺᡢ������ʼ�����,���P������.
���𰸡�
��1���⣺�� ![]()
�� ![]()
�� ![]() ��
�� ![]()
�� ![]() ,
, ![]()
�� m=3��n=6
���A��3,0������B��0,6��
��2���⣺�ӳ�DE��x���ڵ�F���ӳ�FD����G��ʹ��DG=DF������BG
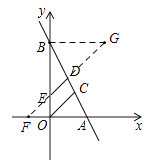
��OE=x
��OCƽ�֡�AOB
���BOC=��AOC=45��
��DE��OC
���EFO=��FEO=��BEG=��BOC=��AOC=45��
��OE=OF=x
�ڡ�ADF�͡�BDG��
�� 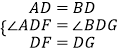
���ADF�ա�BDG��SAS��
��BG=AF=3+x����G=��AFE=45��
���G=��BEG=45��
��BG=BE=6-x
��6-x=3+x
��ã�x=1.5
��OE=1.5
��3���⣺�ֱ����F��P��FM��y���ڵ�M��PN��y���ڵ�N
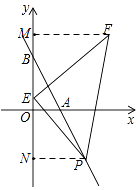
���E��0��m��
�ߵ�P������Ϊ��x��-2x+6��
��PN=x��EN=m+2x-6
�ߡ�PEF=90��
���PEN+��FEM=90��
��FM��y��
���MFE+��FEM=90��
���PEN=��MFE
�ڡ�EFM�͡�PEN��
�� 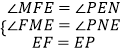
���EFM�ա�PEN��AAS��
��ME=NP=x��FM=EN=m+2x-6
���F��m+2x-6��m+x��
��F�����������������
��m+2x-6=m+x
��ã�x=6
���P��6��-6��
����������1����������õ�ƽ��+����ֵ=0����ƽ���;���ֵ�ķǸ��ԣ��õ�n-6=0��n-2m=0���õ���A����B�����ꣻ��2�����ݽ�ƽ���ߺ�ƽ���ߵ����ʣ�����SAS�õ���ADF�ա�BDG���õ���Ӧ�ߡ���Ӧ����ȣ����OE��ֵ����3������ͼ�κ���֪��������AAS�õ���EFM�ա�PEN���õ���Ӧ����ȣ���F��ĺ���������������ȣ������P������.

 ��˼άС�ھ�100����ҵ��ϵ�д�
��˼άС�ھ�100����ҵ��ϵ�д� ��ʦָ��һ��ͨϵ�д�
��ʦָ��һ��ͨϵ�д�����Ŀ������1��Ϊ������1����ȫ��43��ͬѧij����ѧ����ɼ���ͳ�ƽ����������˵����ȷ���ǣ� ��
�ɼ����֣� | 70 | 80 | 90 |
�������ˣ� | 5 | 10 | 7 |
Ů�����ˣ� | 4 | 13 | 4 |
A��������ƽ���ɼ�����Ů����ƽ���ɼ�
B��������ƽ���ɼ�С��Ů����ƽ���ɼ�
C�������ɼ�����λ������Ů���ɼ�����λ��
D�������ɼ�����λ��С��Ů���ɼ�����λ��