题目内容
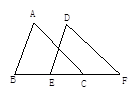
已知:如图,梯形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.
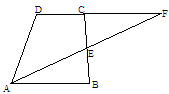
(1)求证:△ABE≌△FCE ;
(2)若BC⊥AB,且BC=16,AB=17,求AF的长.

(1)求证:△ABE≌△FCE ;
(2)若BC⊥AB,且BC=16,AB=17,求AF的长.
(1)通过角角边来证明△ABE≌△FCE (2)34
试题分析:(1)证明:
∵E为BC的中点
∴BE=CE
∵AB∥CD
∴∠BAE=∠F ∠B=∠FCE
∴△ABE≌△FCE
(2)解:由(1)可得:△ABE≌△FCE
∴CE=AB=15,CE=BE=8,AE=EF
∵∠B=∠BCF=90°
根据勾股定理得AE=17
∴AF=34
点评:本题考查三角形全等,掌握全等三角形的判定方法,并会证明
试题分析:(1)证明:
∵E为BC的中点
∴BE=CE
∵AB∥CD
∴∠BAE=∠F ∠B=∠FCE
∴△ABE≌△FCE
(2)解:由(1)可得:△ABE≌△FCE
∴CE=AB=15,CE=BE=8,AE=EF
∵∠B=∠BCF=90°
根据勾股定理得AE=17
∴AF=34
点评:本题考查三角形全等,掌握全等三角形的判定方法,并会证明

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目

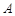 、
、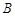 、
、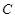 三点均在
三点均在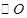 上,且
上,且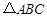 是等边三角形.
是等边三角形.
 是
是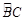 上一点,连接
上一点,连接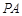 、
、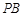 、
、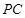 .探究
.探究