题目内容
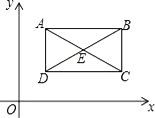
【题目】如图,在平面直角坐标系中,点A(2,n),B(m,n)(m>2),D(p,q)(q<n),点B,D在直线y=![]() x+1上.四边形ABCD的对角线AC,BD相交于点E,且AB∥CD,CD=4,BE=DE,△ABD的面积是4.求证:四边形ABCD是矩形.
x+1上.四边形ABCD的对角线AC,BD相交于点E,且AB∥CD,CD=4,BE=DE,△ABD的面积是4.求证:四边形ABCD是矩形.
【答案】证明见试题解析.
【解析】试题分析:首先利用对角线互相平分的四边形是平行四边形判定该四边形为平行四边形,然后根据△ABE的面积得到整个四边形的面积和AD的长,根据平行四边形的面积计算方法得当DA⊥AB即可判定矩形.
试题解析:作EF⊥AB于点F,∵AB∥CD,∴∠1=∠2,∠3=∠4,在△ABE和△CDE中,∵∠1=∠2,∠3=∠4,BD=CE,∴△ABE≌△CDE,∴AE=CE,∴四边形ABCD是平行四边形,∵CD=4,△AEB的面积是2,∴EF=1,∴AD=2EF=2,∵平行四边形ABCD的面积为△ABE的面积的4倍,∴S四边形ABCD=8,∴DA⊥AB,∴四边形ABCD是矩形.


练习册系列答案
相关题目

