��Ŀ����
����Ŀ������4��23�գ��ǵ�16����������գ�ijУΪ�˽�ѧ��ÿ�ܿ��������Ķ���ʱ�䣬�ڱ�У�����ȡ������ѧ�������ʾ����飬�ֽ����������Ƴ���ͼ��������ͳ��ͼ���������ͼ���е���Ϣ�����������
��� | ѧϰʱ��x��h�� | Ƶ���������� |
A | 0��x��1 | 8 |
B | 1��x��2 | 24 |
C | 2��x��3 | 32 |
D | 3��x��4 | n |
E | 4Сʱ���� | 4 |

��1�����е�n���� ������λ�������� ���飬����ͳ��ͼ��B���Ӧ��Բ�Ľ�Ϊ�� ������
��2���벹ȫƵ���ֲ�ֱ��ͼ��
��3����У���ٿ����ÿ���ʱ����������Ķ��Ľ����ᣬ�ƻ���E��ѧ�������ѡ�����˽��о�����ܣ���֪E�������ѧ���У��ߡ����꼶����1�ˣ����꼶��2�ˣ����û���״ͼ�����б������ȡ������ѧ�������Ծ��꼶�ĸ��ʣ�
���𰸡���1��12��C��108����2����ͼ����������3����ȡ������ѧ�������Ծ��꼶�ĸ���Ϊ![]() ��
��
��������
��1�������������������������15%���Ե������������ɵó�n��Ȼ�������λ���Ķ����һ�������λ�����������鼴�ɣ������B��ռ�������İٷֱȳ���360�㼴�ɵó�����Ӧ��Բ�ĽǶ�����
��2���ɣ�1���ɵ�n��ֵ���ݴ˽�һ����ȫͼ�μ��ɣ�
��3��������״ͼ��Ȼ���һ��������ʼ���.
��1�������������Ϊ8��10%��80��
��n��15%��80��12��
���ڹ���80�����ݣ�
����λ��Ϊ��40��41�����ݵ�ƽ����������40��41�����ݾ�����C�飬
����λ������C�飬
����ͳ��ͼ��B���Ӧ��Բ�Ľ�Ϊ![]() ��360����108����
��360����108����
�ʴ�Ϊ��12��C��108��
��2������ͼ��ʾ��

��3������״ͼ���£�

��12�ֿ��ܣ���ȡ������ѧ�������Ծ��꼶����2�ֿ��ܣ�
��P������ѧ�����Ǿ��꼶����![]() ��
��
�𣺳�ȡ������ѧ�������Ծ��꼶�ĸ���Ϊ![]() ��
��

����Ŀ���ס���������Ա�μ����ѵ����ÿ�����10�Σ��ɼ��ֱ����£�

����������Ϣ�����������������£�
ƽ���ɼ�/�� | ��λ��/�� | ����/�� | ���� | |
�� | a | 7 | 7 | 1.2 |
�� | 7 | b | 8 | c |
��1��a��_____��b��_____��c��_____��
��2����գ�����������������������
�ٴ�ƽ��������λ���ĽǶ����Ƚϣ��ɼ��Ϻõ���_____��
�ڴ�ƽ�����������ĽǶ����Ƚϣ��ɼ��Ϻõ���_____��
�۳ɼ���Խ��ȶ�����_____��
����Ŀ��������ȫ��������������У�ij����Ϊ���˽����������������֪ʶ��������е��飮����A��B��С���ֱ���500�������������и������ȡ50������������֪ʶ���ԣ������ɼ����������õ�������Ϣ��
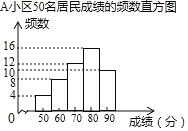
����Ϣһ��AС��50������ɼ���Ƶ��ֱ��ͼ��ͼ��ÿһ�麬ǰһ���߽�ֵ��������һ���߽�ֵ����
����Ϣ����ͼ�У��������ҵ�����ijɼ�����
75 | 75 | 79 | 79 | 79 | 79 | 80 | 80 |
81 | 82 | 82 | 83 | 83 | 84 | 84 | 84 |
����Ϣ����A��B��С����50������ɼ���ƽ��������λ���������������ʣ�80�ּ�����Ϊ���㣩��������������£����ֿ�ȱ����
С�� | ƽ���� | ��λ�� | ���� | ������ | ���� |
A | 75.1 | 79 | 40% | 277 | |
B | 75.1 | 77 | 76 | 45% | 211 |
����������Ϣ���ش��������⣺
��1����AС��50������ɼ�����λ����
��2�������AС��500���������ܳ���ƽ�������ж����ˣ�
��3���뾡���Ӷ���ǶȱȽϡ�����A��B��С������������������֪ʶ�������