题目内容
(2012•锡山区一模)如图,若正方形ABCD的四个顶点恰好分别在四条平行线l1、l2、l3、l4上,设这四条直线中相邻两条之间的距离依次为h1、h2、h3(h1>0,h2>0,h3>0).
(1)求证:h1=h3;
(2)现在平面直角坐标系内有四条直线l1、l2、l3、x轴,且l1∥l2∥l3∥x轴,若相邻两直线间的距离为1,2,1,点A(4,4)在l1,能否在l2、l3、x轴上各找一点B、C、D,使以这四个点为顶点的四边形为正方形?若能,请直接写出B、C、D的坐标;若不能,请说明理由.

(1)求证:h1=h3;
(2)现在平面直角坐标系内有四条直线l1、l2、l3、x轴,且l1∥l2∥l3∥x轴,若相邻两直线间的距离为1,2,1,点A(4,4)在l1,能否在l2、l3、x轴上各找一点B、C、D,使以这四个点为顶点的四边形为正方形?若能,请直接写出B、C、D的坐标;若不能,请说明理由.

分析:(1)过A点作AF⊥l3分别交l2、l3于点E、F,过C点作CG⊥l3交l3于点G,l2∥l3,再证出∠1=∠4,△ABE≌△CDG,即可得出h1=h3,
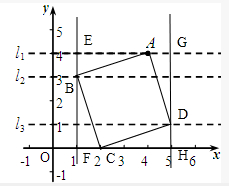
(2)在l1上截取AE=1+2=3,过点E作l1的垂线,交l2于点B,交x轴于点F,在x 轴上截取FC=1,在l1上截取AG=1,过G作l1的垂线交l3于点D,连接AB,BC,CD,DA则四边形ABCD为正方形,
(2)在l1上截取AE=1+2=3,过点E作l1的垂线,交l2于点B,交x轴于点F,在x 轴上截取FC=1,在l1上截取AG=1,过G作l1的垂线交l3于点D,连接AB,BC,CD,DA则四边形ABCD为正方形,
解答: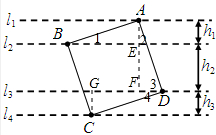 (1)证明:过A点作AF⊥l3分别交l2、l3于点E、F,过C点作CG⊥l3交l3于点G,
(1)证明:过A点作AF⊥l3分别交l2、l3于点E、F,过C点作CG⊥l3交l3于点G,
∵l2∥l3,
∴∠2=∠3,
∵∠1+∠2=90°,∠4+∠3=90°,
∴∠1=∠4,
∵在△ABE和△CDG中,
,
∴△ABE≌△CDG(AAS),
∴AE=CG,
即h1=h3.
(2)解:可以在l1、l2、l3、x轴上找点B,C,D,使四边形ABCD为正方形.
画法如下:
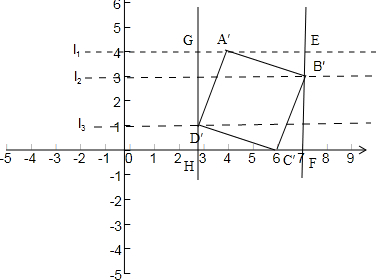 1、在l1上截取AE=1+2=3,过点E作l1的垂线,交l2于点B,交x轴于点F,
1、在l1上截取AE=1+2=3,过点E作l1的垂线,交l2于点B,交x轴于点F,
2、在x 轴上截取FC=1,
3、在l1上截取AG=1,过G作l1的垂线交l3于点D,
4、连接AB,BC,CD,DA则四边形ABCD为正方形,
其中B(1,3),C(2,0),D(5,1)或B’(7,3),C’(6,0),D’(3,1).
 (1)证明:过A点作AF⊥l3分别交l2、l3于点E、F,过C点作CG⊥l3交l3于点G,
(1)证明:过A点作AF⊥l3分别交l2、l3于点E、F,过C点作CG⊥l3交l3于点G,∵l2∥l3,
∴∠2=∠3,
∵∠1+∠2=90°,∠4+∠3=90°,
∴∠1=∠4,
∵在△ABE和△CDG中,

|
∴△ABE≌△CDG(AAS),
∴AE=CG,
即h1=h3.
(2)解:可以在l1、l2、l3、x轴上找点B,C,D,使四边形ABCD为正方形.
画法如下:
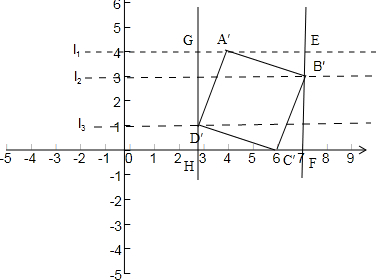 1、在l1上截取AE=1+2=3,过点E作l1的垂线,交l2于点B,交x轴于点F,
1、在l1上截取AE=1+2=3,过点E作l1的垂线,交l2于点B,交x轴于点F,2、在x 轴上截取FC=1,
3、在l1上截取AG=1,过G作l1的垂线交l3于点D,
4、连接AB,BC,CD,DA则四边形ABCD为正方形,
其中B(1,3),C(2,0),D(5,1)或B’(7,3),C’(6,0),D’(3,1).
点评:此题考查了四边形综合,用到的知识点是正方形的性质、全等三角形的判定与性质、平行线的性质等,关键是根据题意画出图形.

练习册系列答案
相关题目