题目内容
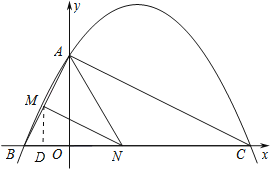
【题目】如图,已知二次函数y=ax2+![]() x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.

(1)请直接写出二次函数y=ax2+![]() x+c的表达式;
x+c的表达式;
(2)判断△ABC的形状,并说明理由;
(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请直接写出此时点N的坐标;
(4)若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标.
【答案】(1)y=﹣![]() x2+
x2+![]() x+4;(2)△ABC是直角三角形.(3)点N的坐标分别为(﹣8,0)、(8﹣4
x+4;(2)△ABC是直角三角形.(3)点N的坐标分别为(﹣8,0)、(8﹣4![]() ,0)、(3,0)、(8+4
,0)、(3,0)、(8+4![]() ,0).(4)当△AMN面积最大时,N点坐标为(3,0).
,0).(4)当△AMN面积最大时,N点坐标为(3,0).
【解析】
试题分析:(1)根据待定系数法即可求得;
(2)根据抛物线的解析式求得B的坐标,然后根据勾股定理分别求得AB2=20,AC2=80,BC10,然后根据勾股定理的逆定理即可证得△ABC是直角三角形.
(3)分别以A、C两点为圆心,AC长为半径画弧,与x轴交于三个点,由AC的垂直平分线与x轴交于一个点,即可求得点N的坐标;
(4)设点N的坐标为(n,0),则BN=n+2,过M点作MD⊥x轴于点D,根据三角形相似对应边成比例求得MD=![]() (n+2),然后根据S△AMN=S△ABN﹣S△BMN
(n+2),然后根据S△AMN=S△ABN﹣S△BMN
得出关于n的二次函数,根据函数解析式求得即可.
解:(1)∵二次函数y=ax2+![]() x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),
x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),
∴![]() ,
,
解得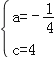 .
.
∴抛物线表达式:y=﹣![]() x2+
x2+![]() x+4;
x+4;
(2)△ABC是直角三角形.
令y=0,则﹣![]() x2+
x2+![]() x+4=0,
x+4=0,
解得x1=8,x2=﹣2,
∴点B的坐标为(﹣2,0),
由已知可得,
在Rt△ABO中AB2=BO2+AO2=22+42=20,
在Rt△AOC中AC2=AO2+CO2=42+82=80,
又∵BC=OB+OC=2+8=10,
∴在△ABC中AB2+AC2=20+80=102=BC2
∴△ABC是直角三角形.
(3)∵A(0,4),C(8,0),
∴AC=![]() =4
=4![]() ,
,
①以A为圆心,以AC长为半径作圆,交x轴于N,此时N的坐标为(﹣8,0),
②以C为圆心,以AC长为半径作圆,交x轴于N,此时N的坐标为(8﹣4![]() ,0)或(8+4
,0)或(8+4![]() ,0)
,0)
③作AC的垂直平分线,交x轴于N,此时N的坐标为(3,0),
综上,若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,点N的坐标分别为(﹣8,0)、(8﹣4![]() ,0)、(3,0)、(8+4
,0)、(3,0)、(8+4![]() ,0).
,0).
(4)设点N的坐标为(n,0),则BN=n+2,过M点作MD⊥x轴于点D,
∴MD∥OA,
∴△BMD∽△BAO,
∴![]() =
=![]() ,
,
∵MN∥AC
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵OA=4,BC=10,BN=n+2
∴MD=![]() (n+2),
(n+2),
∵S△AMN=S△ABN﹣S△BMN
=![]() BNOA﹣
BNOA﹣![]() BNMD
BNMD
=![]() (n+2)×4﹣
(n+2)×4﹣![]() ×
×![]() (n+2)2
(n+2)2
=﹣![]() (n﹣3)2+5,
(n﹣3)2+5,
∴当△AMN面积最大时,N点坐标为(3,0).

【题目】近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神,对部分学生的每天体育锻炼时间进行了调查统计.以下是本次调查结果的统计表和统计图.
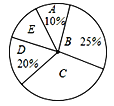
组别 | A | B | C | D | E |
时间t(分钟) | t<40 | 40≤t<60 | 60≤t<80 | 80≤t<100 | t≥100 |
人数 | 12 | 30 | a | 24 | 12 |
(1)本次被调查的学生数是 人;
(2)统计表中a的值为 ;
(3)各组人数的众数是 ;
(4)根据调查结果,请你估计该校2400名学生中每天体育锻炼时间不少于1小时的学生人数.