题目内容
如图:已知点C是线段AB上的点,△ACD与△BCE都是正三角形,F、G、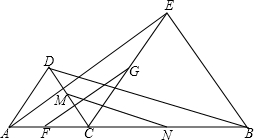 M、N分别是线段AC、CE、CD、CB的中点,
M、N分别是线段AC、CE、CD、CB的中点,求证:FG=MN.
分析:根据等边三角形的性质以及等量代换可知∠ACD+∠DCE=∠BCE+∠DCE,再根据全等三角形的判定即可证明△ACE≌△DCB,可知AE=BD,再根据中点的定义即可证明FG=MN.
解答:证明:∵△ACD与△BCE都是正三角形,
∴AC=DC,EC=BC,∠ACD=∠BCE,
∴∠ACD+∠DCE=∠BCE+∠DCE,
即∠ACE=∠BCD,
∴△ACE≌△DCB,
∴AE=BD,
又∵F、G、M、N分别是线段AC、CE、CD、CB的中点,
∴FG是△ACE的中位线,MN是△DCB的中位线,
∴FG=
AE,MN=
BD,
∴FG=MN.
∴AC=DC,EC=BC,∠ACD=∠BCE,
∴∠ACD+∠DCE=∠BCE+∠DCE,
即∠ACE=∠BCD,
∴△ACE≌△DCB,
∴AE=BD,
又∵F、G、M、N分别是线段AC、CE、CD、CB的中点,
∴FG是△ACE的中位线,MN是△DCB的中位线,
∴FG=
| 1 |
| 2 |
| 1 |
| 2 |
∴FG=MN.
点评:本题主要考查了等边三角形的性质,全等三角形的判定与性质以及三角形的中位线定理,比较综合,难度适中.

练习册系列答案
相关题目
 如图,已知点C是线段AB的中点,且AC=3,则AB的长为( )
如图,已知点C是线段AB的中点,且AC=3,则AB的长为( )A、
| ||
| B、3 | ||
| C、6 | ||
| D、12 |
 如图,已知点P是线段AB的黄金分割点,且AB=
如图,已知点P是线段AB的黄金分割点,且AB= 如图,已知点C是线段AD的中点,AB=10cm,BD=4cm,则BC=
如图,已知点C是线段AD的中点,AB=10cm,BD=4cm,则BC= 如图,已知点M是线段AB的中点,N是线段AM上的点,且满足AN:MN=1:2,若AN=2cm,则线段AB=( )
如图,已知点M是线段AB的中点,N是线段AM上的点,且满足AN:MN=1:2,若AN=2cm,则线段AB=( ) 如图,已知点C是线段AB上一点,点M,N分别是线段AC,BC的中点,则MN=
如图,已知点C是线段AB上一点,点M,N分别是线段AC,BC的中点,则MN=