题目内容
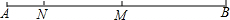如图，已知点M是线段AB的中点，N是线段AM上的点，且满足AN：MN=1：2，若AN=2cm，则线段AB=（ ）分析：这是一道线段比例问题，由AN的长度通过线段比可以求出MN，从而可以求出AM的长度，再利用线段中点的定义就可以求出AB．
解答：解：∵AN：MN=1：2，且AN=2，
∴2：MN=1：2，
∴MN=4cm，
∴AM=6cm．
∵M是线段AB的中点，
∴AB=2AM，
∴AB=12cm，故D答案正确．
故选D．
∴2：MN=1：2，
∴MN=4cm，
∴AM=6cm．
∵M是线段AB的中点，
∴AB=2AM，
∴AB=12cm，故D答案正确．
故选D．
点评：本题是一道求有关线段长度的几何问题，考查了利用线段的比求线段的长度，线段中点的意义和运用．
练习册系列答案
相关题目
如图，已知点P是线段AB的黄金分割点，且AB=
如图，已知点C是线段AD的中点，AB=10cm，BD=4cm，则BC=
如图，已知点C是线段AB上一点，点M，N分别是线段AC，BC的中点，则MN=
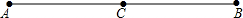如图，已知点C是线段AB的中点，且AC=3，则AB的长为（ ）A、
| ||
| B、3 | ||
| C、6 | ||
| D、12 |