题目内容
【题目】如图，在矩形ABCD中，AB=8cm，BC=6cm，动点E从点A出发．以2cm/s的速度沿射线AD方向运动，以AE为底边，在AD的右侧作等腰直角角形AEF，当点F落在射线BC上时，点E停止运动，设△AEF与矩形ABCD重叠部分的面积为S，运动的时间为t（s）．
（1）当t为何值时，点F落在射线BC上；
（2）当线段CD将△AEF的面积二等分时，求t的值；
（3）求S与t的函数关系式；
（4）当S=17时，求t的值．
【答案】（1）8（2）6（3）S=
（4）5
【解析】
试题分析：（1）由矩形的性质和等腰直角三角形的性质得出FH=8cm，再由运动得出FH=t，即可；
（2）由等腰直角三角形的性质得出斜边上的高也是中线，根据三角形的中线把三角形AEF面积平分，判断出点F在CD上，即可；
（3）分三种情况先利用矩形和运动的特点显示出三角形高，底边和梯形的上下底，高，再利用三角形和梯形的面积公式求解；
（4）先判断出面积是17时，运动时间在3＜t≤6内，再直接代入函数关系式中，即可．
试题解析：（1）如图1，
过点F作FH⊥AD于H，
在矩形ABCD中，AB=8cm，BC=6cm，∠BAD=90°，
∵点F落在射线BC上，
∴FH=8cm，
∴t=8s，
（2）如图2，
∵△AEF是等腰直角三角形，
∴AE边上的高线也是该边的中线，
∴点F在边CD上时，CD将△AEF的面积二等分，
∵FD是直角三角形的斜边的直线，
∴由运动知，FD=AD=6=t，
∴t=6s，
（3）当0＜t≤3时，如图3，
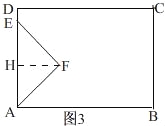
过点F作FH⊥AD，
由运动知，AE=2t，
∴FH=
AE=t，
∴S=
AE×FH=t2，
当3＜t≤6时，如图4，
过点F作FH⊥AD，
由运动知，AE=2t，
∴DG=DE=2t﹣6，FH=t，DH=6﹣t，
∴S=
S△AEF+S梯形DHFG=×AE×FH+（DG+FH）×DH=××2t×t+（2t﹣6+t）×（6﹣t）=﹣t2+12t﹣18，
当6＜t≤8时，如图5，
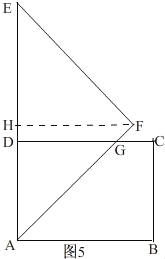
过点F作FH⊥AD，
∴DG=AD=6
∴S=S△ADG=AD×GD=18；
∴S=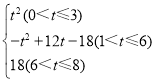
，
（4）由函数关系式知，S=17的运动时间在3＜t≤6中，
将S=17代入S=﹣t2+12t﹣18中，
∴﹣t2+12t﹣18=17，
∴t=7（舍）或t=5
∴当S=17时，t的值为5s．
