题目内容
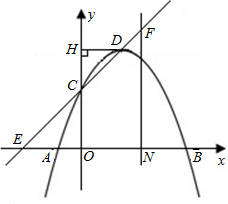 已知抛物线y=ax2-2ax-3a(a<0)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为抛物线的顶点.
已知抛物线y=ax2-2ax-3a(a<0)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为抛物线的顶点.
(1)求A、B的坐标;
(2)过点D作DH丄y轴于点H,若DH=HC,求a的值和直线CD的解析式;
(3)在第(2)小题的条件下,直线CD与x轴交于点E,过线段OB的中点N作NF丄x轴,并交直线CD于点F,则直线NF上是否存在点M,使得点M到直线CD的距离等于点M到原点O的距离?若存在,求出点M的坐标;若不存在,请说明理由.
解:(1)由y=0得,ax2-2ax-3a=0,
∵a≠0,
∴x2-2x-3=0,
解得x1=-1,x2=3,
∴点A的坐标(-1,0),点B的坐标(3,0);
(2)由y=ax2-2ax-3a,令x=0,得y=-3a,
∴C(0,-3a),
又∵y=ax2-2ax-3a=a(x-1)2-4a,
得D(1,-4a),
∴DH=1,CH=-4a-(-3a)=-a,
∴-a=1,
∴a=-1,
∴C(0,3),D(1,4),
设直线CD的解析式为y=kx+b,把C、D两点的坐标代入得, ,
,
解得 ,
,
∴直线CD的解析式为y=x+3;
(3)存在.
由(2)得,E(-3,0),
∵点B的坐标(3,0),N是线段OB的中点,
∴N( ,0)
,0)
∴F( ,
, ),EN=
),EN= ,
,
作MQ⊥CD于Q,
设存在满足条件的点M( ,m),则FM=
,m),则FM= -m,
-m,
EF= =
= ,MQ=OM=
,MQ=OM=
由题意得:Rt△FQM∽Rt△FNE,
∴ =
= ,
,
即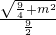 =
= ,
,
∴2( +m2)=(
+m2)=( -m)2,
-m)2,
整理得4m2+36m-63=0,
∴m2+9m=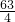 ,
,
m2+9m+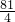 =
=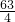 +
+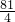
(m+ )2=
)2=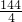
m+ =±
=±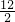
∴m1= ,m2=-
,m2=- ,
,
∴点M的坐标为M1( ,
, ),M2(
),M2( ,-
,- ).
).
分析:(1)令y=0求得x的值,从而得出点A、B的坐标;
(2)令x=0,则y=-3a,求得点C、D的坐标,设直线CD的解析式为y=kx+b,把C、D两点的坐标代入,求出直线CD的解析式;
(3)设存在,作MQ⊥CD于Q,由Rt△FQM∽Rt△FNE,得 =
= ,及可得出关于m的一元二次方程,求出方程的解,即可得出点M的坐标.
,及可得出关于m的一元二次方程,求出方程的解,即可得出点M的坐标.
点评:本题是二次函数的综合题型,其中涉及的知识点有一元二次方程的解法.在求有关存在不存在问题时要注意先假设存在,再讨论结果.
∵a≠0,
∴x2-2x-3=0,
解得x1=-1,x2=3,
∴点A的坐标(-1,0),点B的坐标(3,0);
(2)由y=ax2-2ax-3a,令x=0,得y=-3a,
∴C(0,-3a),
又∵y=ax2-2ax-3a=a(x-1)2-4a,
得D(1,-4a),
∴DH=1,CH=-4a-(-3a)=-a,
∴-a=1,
∴a=-1,
∴C(0,3),D(1,4),
设直线CD的解析式为y=kx+b,把C、D两点的坐标代入得,
 ,
,解得
 ,
,∴直线CD的解析式为y=x+3;
(3)存在.

由(2)得,E(-3,0),
∵点B的坐标(3,0),N是线段OB的中点,
∴N(
 ,0)
,0)∴F(
 ,
, ),EN=
),EN= ,
,作MQ⊥CD于Q,
设存在满足条件的点M(
 ,m),则FM=
,m),则FM= -m,
-m,EF=
 =
= ,MQ=OM=
,MQ=OM=
由题意得:Rt△FQM∽Rt△FNE,
∴
 =
= ,
,即
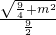 =
= ,
,∴2(
 +m2)=(
+m2)=( -m)2,
-m)2,整理得4m2+36m-63=0,
∴m2+9m=
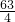 ,
,m2+9m+
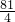 =
=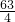 +
+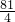
(m+
 )2=
)2=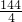
m+
 =±
=±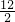
∴m1=
 ,m2=-
,m2=- ,
,∴点M的坐标为M1(
 ,
, ),M2(
),M2( ,-
,- ).
).分析:(1)令y=0求得x的值,从而得出点A、B的坐标;
(2)令x=0,则y=-3a,求得点C、D的坐标,设直线CD的解析式为y=kx+b,把C、D两点的坐标代入,求出直线CD的解析式;
(3)设存在,作MQ⊥CD于Q,由Rt△FQM∽Rt△FNE,得
 =
= ,及可得出关于m的一元二次方程,求出方程的解,即可得出点M的坐标.
,及可得出关于m的一元二次方程,求出方程的解,即可得出点M的坐标.点评:本题是二次函数的综合题型,其中涉及的知识点有一元二次方程的解法.在求有关存在不存在问题时要注意先假设存在,再讨论结果.

练习册系列答案
相关题目
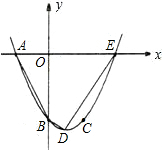 与x轴的另一个交点为E.
与x轴的另一个交点为E.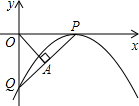 如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=
如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=