��Ŀ����
���壺���һ��y��x�ĺ���ͼ��ƽ�ƺ�����ij������������ͼ���غϣ���ô�����������y��x�ġ�������ƽ�ƺ����������磺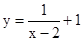 ��ͼ������ƽ��2����λ��������ƽ��1����λ�õ�
��ͼ������ƽ��2����λ��������ƽ��1����λ�õ�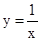 ��ͼ����
��ͼ����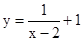 ��y��x�ġ�������ƽ�ƺ�������
��y��x�ġ�������ƽ�ƺ�������
��1�������ε����߷ֱ���2cm��3cm���������߷ֱ�����x��cm����y��cm���õ����¾��ε����Ϊ8cm2����y��x�ĺ�������ʽ�����ж���������Ƿ�Ϊ��������ƽ�ƺ�������
��2����ͼ����ƽ��ֱ������ϵ�У���OΪԭ�㣬����OABC�Ķ���A��C������ֱ�Ϊ��9��0������0��3������D��OA���е㣬����OB��CD���ڵ�E����������ƽ�ƺ����� ��ͼ��B��E���㣮�������������ƽ�ƺ������ı���ʽΪ �������������ƽ�ƺ�������ͼ���ʵ��ı任��ijһ��������������ͼ���غϣ���д����������������ı���ʽ��
��ͼ��B��E���㣮�������������ƽ�ƺ������ı���ʽΪ �������������ƽ�ƺ�������ͼ���ʵ��ı任��ijһ��������������ͼ���غϣ���д����������������ı���ʽ��
��3���ڣ�2���������£���֪���߶�BE�е��һ��ֱ��l�������������ƽ�ƺ�����ͼ����P��Q���㣨P��Q���Ҳࣩ����B��E��P��QΪ������ɵ��ı������Ϊ16���������P�����꣮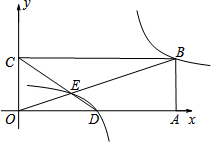
��1��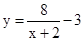 ���ǣ���2��
���ǣ���2�� ��
�� ����3����7��5����15��
����3����7��5����15�� ����
����
���������������1�������¾��ε����Ϊ8cm2�����Կ�������������ɵõ�һ������x��y�ķ��̣����ɱ��γɺ�������ʽ�������ж�.
��2����B��D��������� �����з������a��k��ֵ����������ʽ�������.
�����з������a��k��ֵ����������ʽ�������.
��3���ɷ��������������ĶԳ��ԣ��ı���PEQBΪƽ���ı��Σ���P1��x0��y0��������S��OP1E=S�ı���ONMC-S��OCP1-S��MP1E-S��ONE�������з�����⣮
�����������1���ߣ�x+2����y+3��=8��
��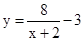 ����ƽ��2����λ��������ƽ��3����λ�õ�
����ƽ��2����λ��������ƽ��3����λ�õ� .
.
��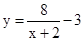 �ǡ�������ƽ�ƺ�������
�ǡ�������ƽ�ƺ�������
��2����B��D��������� �ã�
�ã� ����ã�
����ã�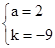 .
.
������ƽ�ƺ������ı���ʽΪ .
.
�ʱ任��ķ�������������ʽΪ .
.
��3����ͼ������P�ڵ�B���ʱ�����߶�BE���е�ΪF���ɷ������������ĶԳ��ԣ��ı���PEQBΪƽ���ı��Σ�
���ı���PEQB�����Ϊ16����S��PFE=4��
��B��9��3����F��6��2���� ��
�� �ġ�������ƽ�ƺ�������
�ġ�������ƽ�ƺ�������
��S��PFE=S��POE=4����E�������ǣ���3��1��.
��E��x��Ĵ��ߣ���BC��x��ֱ���M��N�㣮
S��OP1E=S�ı���ONMC-S��OCP1-S��MP1E-S��ONE��
��P1��x0��y0����
�� ����
���� �����
����� .
.
��P1��1��3����
���P��������7��5����
����P�ڵ�B�Ҳ�ʱ��ͬ���ɵõ�P������Ϊ��15�� ����
����
������������P��������7��5����15�� ����
����
���㣺1.�����������ۺ��⣻2.�¶��壻3.ƽ�Ƶ����ʣ�4.ת��˼��ͷ���˼���Ӧ�ã�


 ͼ�����֧�ϣ���PB��x�ڵ�C��PA��y�ڵ�D��AB�ֱ���x�ᣬy���ཻ�ڵ�E��F����֪B��1��3����
ͼ�����֧�ϣ���PB��x�ڵ�C��PA��y�ڵ�D��AB�ֱ���x�ᣬy���ཻ�ڵ�E��F����֪B��1��3���� ʱ�����P�����꣮
ʱ�����P�����꣮
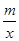 ��x��0����ͼ���ڵ�P��n��2������x�ύ�ڵ�A����4��0������y�ύ�ڵ�C��PB��x���ڵ�B����AC=BC��
��x��0����ͼ���ڵ�P��n��2������x�ύ�ڵ�A����4��0������y�ύ�ڵ�C��PB��x���ڵ�B����AC=BC��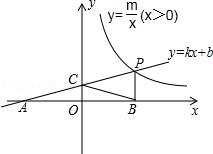
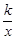 ��ͼ��BC��AB�ڵ�D��E��
��ͼ��BC��AB�ڵ�D��E��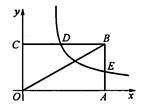
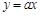 ��ͼ���뷴��������
��ͼ���뷴�������� ��ͼ���ڵ�
��ͼ���ڵ�
 ȡ��ֵʱ��������������ֵ����������������ֵ��
ȡ��ֵʱ��������������ֵ����������������ֵ��
 �뷴��������
�뷴�������� ��ͼ���ڵ�
��ͼ���ڵ�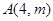 ��
��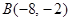 ����
����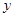 �ύ�ڵ�
�ύ�ڵ� ��(1)
��(1)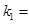 ,
,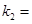 ��
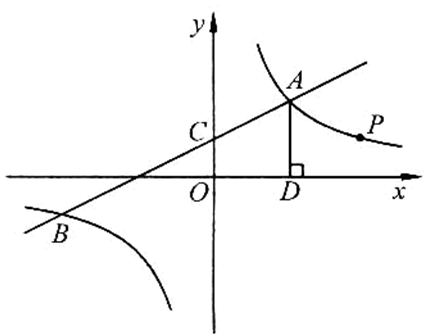
��
 ʱ��
ʱ��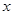 ��ȡֵ��Χ�� ��
��ȡֵ��Χ�� �� ��
��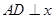 ���ڵ�
���ڵ�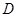 ����
����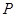 �Ƿ����������ڵ�һ����ͼ����һ��,��ֱ��
�Ƿ����������ڵ�һ����ͼ����һ��,��ֱ��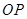 ���߶�
���߶� ���ڵ�
���ڵ�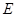 ����
����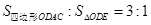 ʱ�����
ʱ�����