题目内容
如图，已知：AE⊥BE，DF⊥CF，AB=CD，CE=BF，求证：∠A=∠D．考点：全等三角形的判定与性质
专题：证明题
分析：由CE=BF，利用等式的性质得到CF=BE，再由CD=AB，利用HL得到直角三角形CDF与直角三角形BAE全等，利用全等三角形对应角相等即可得证．
解答：证明：∵CE=BF，
∴CE+EF=BF+EF，即CF=BE，
在Rt△CDF和Rt△BAE中，
，
∴Rt△CDF≌Rt△BAE（HL），
∴∠A=∠D．
∴CE+EF=BF+EF，即CF=BE，
在Rt△CDF和Rt△BAE中，
|
∴Rt△CDF≌Rt△BAE（HL），
∴∠A=∠D．
点评：此题考查了全等三角形的判定与性质，熟练掌握全等三角形的判定与性质是解本题的关键．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
如图：菱形的周长为8cm，高为| 3 |
| A、3：1 | B、4：1 |
| C、2：1 | D、5：1 |
若-2x2+4x-7=-2（x+m）2+n，则m，n的值为（ ）
| A、m=1，n=-5 |
| B、m=-1，n=-5 |
| C、m=1，n=9 |
| D、m=-1，n=-9 |
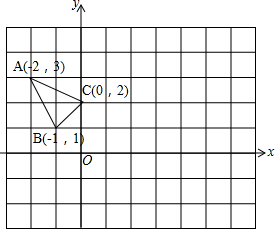△ABC在平面直角坐标系xOy中的位置如图．
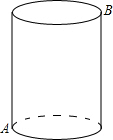如图，圆柱的底圆面积是
如图，在四边形ABCD中，AB＞CD，E、F分别是对角线BD、AC的中点，求证：EF＞
如图是某市区四个景点或单位（A为商店，C为工人文化宫，F为牌坊，G为市汽车站）的大致平面图．可将方格的边长看作是一个单位长度．