题目内容
【题目】如图1，小敏利用课余时间制作了一个脸盆架，图2是它的截面图，垂直放置的脸盆与架子的交点为A，B，AB=40cm，脸盆的最低点C到AB的距离为10cm，则该脸盆的半径为cm．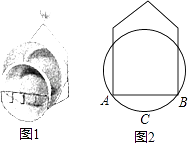
【答案】25
【解析】解；如图，设圆的圆心为O，连接OA，OC，OC与AB交于点D，设⊙O半径为R，
∵OC⊥AB，
∴AD=DB= 
AB=20，∠ADO=90°，
在RT△AOD中，∵OA2=OD2+AD2 ，
∴R2=202+（R﹣10）2 ，
∴R=25．
故答案为25．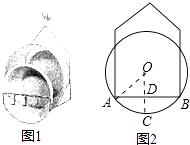
设圆的圆心为O，连接OA，OC，OC与AB交于点D，设⊙O半径为R，在RT△AOD中利用勾股定理即可解决问题．本题考查垂径定理、勾股定理等知识，解题的关键是学会添加常用辅助线，利用勾股定理列方程解决问题，属于中考常考题型．
练习册系列答案
名校课堂系列答案
相关题目
【题目】为了解七年级学生上学期参加社会实践活动的情况，随机抽查A市七年级部分学生参加社会实践活动天数，并根据抽查结果制作了如下不完整的频数分布表和条形统计图．
A市七年级部分学生参加社会实践活动天数的频数分布表
天数 | 频数 | 频率 |
3 | 20 | 0.10 |
4 | 30 | 0.15 |
5 | 60 | 0.30 |
6 | a | 0.25 |
7 | 40 | 0.20 |
A市七年级部分学生参加社会实践活动天数的条形统计图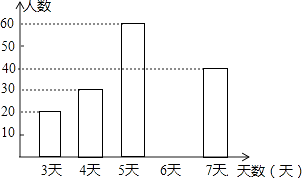
根据以上信息，解答下列问题；
（1）求出频数分布表中a的值，并补全条形统计图．
（2）A市有七年级学生20000人，请你估计该市七年级学生参加社会实践活动不少于5天的人数．
