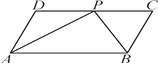
题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,
,![]() 于点
于点![]() 交
交![]() 于
于![]() 点,延长
点,延长![]() 至
至![]() 使
使![]() ,连接
,连接![]() .
.

(1)证明:四边形![]() 是矩形;
是矩形;
(2)当![]() 时,猜想线段
时,猜想线段![]() 、
、![]() 、
、![]() 的数量关系,并证明.
的数量关系,并证明.
【答案】(1)详见解析;(2)![]() ,证明详见解析
,证明详见解析
【解析】
(1)根据平行四边形的性质得到AD∥BC,AD=BC,进而求出AD=FH,再根据平行四边形的判定得出四边形AFHD是平形四边形,最后根据矩形的判定得出即可得到答案;
(2)根据平行四边形的性质得到AB∥CD,求出∠1=∠3,推出AE=AD,再根据正方形的判定和性质得出AD=DH,求出△DAG≌△DHM,最后根据全等三角形的性质得出∠2=∠3=∠HDM,∠AGD=∠M,求出∠M=∠CDM即可得到答案.
(1)∵四边形![]() 是平行四边形
是平行四边形
∴![]() ,
,![]() (平行四边形对边平行且相等),
(平行四边形对边平行且相等),
∵![]()
∴![]() ,
,
∴![]() (等量替换),
(等量替换),
∴四边形![]() 是平行四边形(对边平行且相等的四边形是平行四边形),
是平行四边形(对边平行且相等的四边形是平行四边形),
∵![]() ∴
∴![]() ,
,
∴平行四边形![]() 是矩形;
是矩形;
(2)猜想:![]()
证明:如图,延长![]() 至
至![]() 使
使![]() ,连接
,连接![]() ,
,

∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ∴
∴![]() ,
,
∵![]() 平分
平分![]() ∴
∴![]() ∴
∴![]() ∴
∴![]() ,
,
∵![]() ∴
∴![]() ,
,
∴四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
在△DAG和△DHM中,

∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ;
;

练习册系列答案
 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目