题目内容
若 ,且一元二次方程kx2+ax+b=0有两个实数根,则k的取值范围是 .
,且一元二次方程kx2+ax+b=0有两个实数根,则k的取值范围是 .
 ,且一元二次方程kx2+ax+b=0有两个实数根,则k的取值范围是 .
,且一元二次方程kx2+ax+b=0有两个实数根,则k的取值范围是 .k≤4且k≠0.
试题分析:首先根据非负数的性质求得a、b的值,再由二次函数的根的判别式来求k的取值范围.
∵
 ,
,∴b﹣1=0,
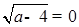 ,
,解得,b=1,a=4;
又∵一元二次方程kx2+ax+b=0有两个实数根,
∴△=a2﹣4kb≥0且k≠0,
即16﹣4k≥0,且k≠0,
解得,k≤4且k≠0;
故答案为:k≤4且k≠0.

练习册系列答案
相关题目

 的根的情况是( )
的根的情况是( )


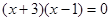
 的一个根为0,则
的一个根为0,则 = .
= . 的两根为a、b,则
的两根为a、b,则 的值是____________.
的值是____________.