题目内容
【题目】在ABCD中,点E,F分别在AB,CD上,∠ADE=∠CBF. 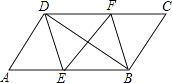
(1)求证:AE=CF;
(2)若DF=BF,求证:EF⊥BD.
【答案】
(1)证明:∵四边形ABCD为平行四边形,
∴AD=BC,∠A=∠C,
在△ADE和△CBF中, 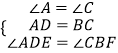 ,
,
∴△ADE≌△CBF(ASA),
∴AE=CF;
(2)证明:∵AE=CF,DF=BF,
∴DF=BE,∵DF∥BE,
∴四边形DEBF是平行四边形,
∴四边形DEBF是菱形,
∴EF⊥BD.
【解析】(1)根据全等三角形的判定定理证明△ADE≌△CBF,即可证得结论;(2)证明四边形DEBF是菱形,即可得出结论.
【考点精析】通过灵活运用平行四边形的性质,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分即可以解答此题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】下列表格是二次函数y=ax2+bx+c(d≠0)的自变量x与函数y的一些对应值,由此可以判断方程ax2+bx+c=0(a≠0)的一个根在( )
x | 6.17 | 6.18 | 6.19 | 6.20 |
y=ax2+bx+c | ﹣0.03 | ﹣0.01 | 0.02 | 0.06 |
A.﹣0.01﹣0.02之间
B.0.02﹣0.06之间
C.6.17﹣6.18之间
D.6.18﹣6.19之间