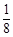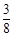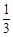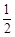题目内容
在一个透明的袋子里,装有相同的四个小球,其上面分别标有数字-1,1,2,3.现从中任意摸出一个小球,将上面的数字作为点A的横坐标,不放回再从中摸出一个小球,将其上面的数字作为A点的纵坐标.
小题1:用树状图或列表法写出A点坐标的所有可能性;(5分)
小题2:求点A在直线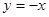 上的概率;(2分)
上的概率;(2分)
小题3:求点A的横坐标、纵坐标之和是偶数的概率.(3分)
小题1:用树状图或列表法写出A点坐标的所有可能性;(5分)
小题2:求点A在直线
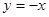 上的概率;(2分)
上的概率;(2分)小题3:求点A的横坐标、纵坐标之和是偶数的概率.(3分)
小题1:-1 1 2 3
 |  | ||||||
 | |||||||
 | |||||||
1 2 3 -1 2 3 -1 1 3 -1 1 2 (3分)
A点坐标的所有可能为:(-1,1)(-1,2)(-1,3)(1,-1)(1,2)
(1,3)(2,-1)(2,1)(2,3)(3,-1)(3,1)(3,2)(5分)
小题2:P(
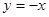 )=
)=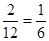 (7分)
(7分)小题3:P(横、纵坐标之和为偶数)=
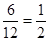
(1)依据题意先用列表法或画树状图法分析所有等可能的出现结果,注意要不重不漏;
(2)注意点M在直线y=-x上,即点M的横、纵坐标相反,求得符合要求的点的个数,利用概率公式求解即可求得答案;
(3)依据题意先用列表法分析所有等可能的出现结果,然后根据概率公式即可求出该事件的概率.
(2)注意点M在直线y=-x上,即点M的横、纵坐标相反,求得符合要求的点的个数,利用概率公式求解即可求得答案;
(3)依据题意先用列表法分析所有等可能的出现结果,然后根据概率公式即可求出该事件的概率.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
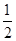
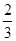
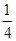
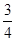
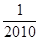 ,则密码位数至少需要 ◆ 位.
,则密码位数至少需要 ◆ 位. ,B转盘指针所指区域内的数字记为
,B转盘指针所指区域内的数字记为 .这样就确定了点P的坐标
.这样就确定了点P的坐标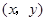 .(1)用列表或画树状图的方法写出点P的所有可能坐标;(2)求点P落在坐标轴上的概率.
.(1)用列表或画树状图的方法写出点P的所有可能坐标;(2)求点P落在坐标轴上的概率.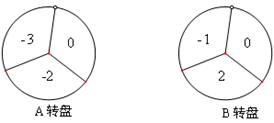
 的概率(4分)
的概率(4分)
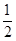 . (B)
. (B)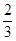 . (C)
. (C)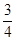 . (D)
. (D)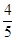 .
.