题目内容
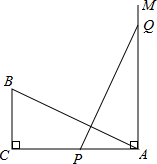
 如图所示,有两个直角三角形△ABC和△QPA按如图位置摆放C,P,A在同一条直线上,并且BC=PA.当QP与AB垂直时,△ABC能和△QPA全等吗,请说明理由.
如图所示,有两个直角三角形△ABC和△QPA按如图位置摆放C,P,A在同一条直线上,并且BC=PA.当QP与AB垂直时,△ABC能和△QPA全等吗,请说明理由.分析:首先根据∠QAP=90°,AB⊥PQ可证出∠PQA=∠BAC,在加上条件BC=AP,∠C=∠QAP=90°,可利用AAS定理证明△ABC和△QPA全等.
解答:△ABC能和△QPA全等;
证明:∵∠QAP=90°,
∴∠PQA+∠QPA=90°,
∵QP⊥AB,
∴∠BAC+∠APQ=90°,
∴∠PQA=∠BAC,
在△ABC和△QPA中,
,
∴△ABC≌△QPA(AAS).
证明:∵∠QAP=90°,
∴∠PQA+∠QPA=90°,
∵QP⊥AB,
∴∠BAC+∠APQ=90°,
∴∠PQA=∠BAC,
在△ABC和△QPA中,
|
∴△ABC≌△QPA(AAS).
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
 25、友情提示:本题有A、B两题,请你任选一题作答,A题满分9分,B题满分12分.若两题都做,只能按A题评分.
25、友情提示:本题有A、B两题,请你任选一题作答,A题满分9分,B题满分12分.若两题都做,只能按A题评分.
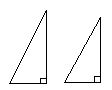
 如图所示,有两个直角三角形△ABC和△QPA按如图位置摆放C,P,A在同一条直线上,并且BC=PA.当QP与AB垂直时,△ABC能和△QPA全等吗,请说明理由.
如图所示,有两个直角三角形△ABC和△QPA按如图位置摆放C,P,A在同一条直线上,并且BC=PA.当QP与AB垂直时,△ABC能和△QPA全等吗,请说明理由.