题目内容
 25、友情提示:本题有A、B两题,请你任选一题作答,A题满分9分,B题满分12分.若两题都做,只能按A题评分.
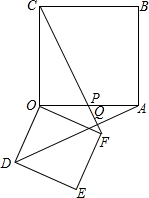
25、友情提示:本题有A、B两题,请你任选一题作答,A题满分9分,B题满分12分.若两题都做,只能按A题评分.(A题)如图所示,四边形OABC与ODEF均为正方形,CF交OA于P,交DA于Q.
(1)求证:AD=CF.
(2)AD与CF垂直吗?说说你的理由.
(3)当正方形ODEF绕O点在平面内旋转时,(1),(2)的结论是否有变化(不需说明理由).
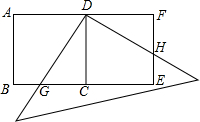
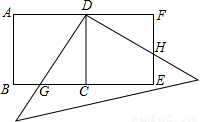
(B题)如图所示,用两个全等的正方形ABCD和CDFE拼成一矩形ABEF,把一个足够大的直角三角尺的直角顶点与这个矩形的边AF的中点D重合,且将直角三角尺绕点D按逆时针方向旋转.

(1)当直角三角尺的两直角边分别与矩形ABEF的两边BE、EF相交于点G、H时,通过观察或测量BG与EH的长度,你能得到什么结论?并证明你的结论.
(2)当直角三角尺的两直角边分别与BE的延长线、EF的延长线相交于点G、H时,你在(1)中得到的结论还成立吗?请画出图形并简要说明理由.
分析:A:(1)可通过证明△AOD和△COF全等.
(2)要证AD⊥CF,就要证明∠APQ+∠OAD=90°,由(1)的全等三角形我们可知:∠OCF=∠OAD,而对顶角∠CPO=∠OAD,因此可得出:∠APQ+∠OAD=∠OCF+∠CPO=90°,也就是∠AQP=90°,那么垂直就证出来了.
(3)结论是不会改变的,因为不管怎么变化都要经过证明三角形AOD和COF全等来得出,而这两个三角形的全等条件中,两组对应边都是正方形的边长,不会改变,而这两组对应边的夹角都是90°加上或减去同一个角,因此也相等,由此可得出,这两个三角形必然全等,(1)(2)的条件自然成立.
B:(1)要证BG=EH,关键是要证明CG=FH,也就是必须得出三角形CDG和FDH全等.
(2)同(1)的证法完全一样.
(2)要证AD⊥CF,就要证明∠APQ+∠OAD=90°,由(1)的全等三角形我们可知:∠OCF=∠OAD,而对顶角∠CPO=∠OAD,因此可得出:∠APQ+∠OAD=∠OCF+∠CPO=90°,也就是∠AQP=90°,那么垂直就证出来了.
(3)结论是不会改变的,因为不管怎么变化都要经过证明三角形AOD和COF全等来得出,而这两个三角形的全等条件中,两组对应边都是正方形的边长,不会改变,而这两组对应边的夹角都是90°加上或减去同一个角,因此也相等,由此可得出,这两个三角形必然全等,(1)(2)的条件自然成立.
B:(1)要证BG=EH,关键是要证明CG=FH,也就是必须得出三角形CDG和FDH全等.
(2)同(1)的证法完全一样.
解答: (A题)
(A题)
(1)证明:∵四边形OABC与ODEF均为正方形,
∴AO=CO,∠AOC=∠DOF=90°,OD=OF,
∴∠AOD=∠COF,
∴△AOD≌△COF,
∴AD=CF.
(2)AD⊥CF
理由为:∵△AOD≌△COF,
∴∠OCF=∠OAD,
∴∠APQ+∠OAD=∠OCF+∠CPO=90°,
∴∠AQP=90°,
即AD⊥CF.
(3)当正方形ODEF绕O点在平面内旋转时,(1)(2)的结论不会发生变化.
(B题)
解:
(1)BG=EH,
∵四边形ABCD和CDFE都是正方形,
∴DC=DF,∠DCG=∠DFH=∠FDC=90°,
∵∠CDG+∠CDH=∠CDH+∠FDH=90°,
∴∠CDG=∠FDH,
∴△CDG≌△FDH,
∴CG=FH,
∵BC=EF,
∴BG=EH.
(2)结论BG=EH仍然成立.
同理可证△CDG≌△FDH,
∴CG=FH,
∵BC=EF,
∴BG=EH.
 (A题)
(A题)(1)证明:∵四边形OABC与ODEF均为正方形,
∴AO=CO,∠AOC=∠DOF=90°,OD=OF,
∴∠AOD=∠COF,
∴△AOD≌△COF,
∴AD=CF.
(2)AD⊥CF
理由为:∵△AOD≌△COF,
∴∠OCF=∠OAD,
∴∠APQ+∠OAD=∠OCF+∠CPO=90°,
∴∠AQP=90°,
即AD⊥CF.
(3)当正方形ODEF绕O点在平面内旋转时,(1)(2)的结论不会发生变化.
(B题)
解:
(1)BG=EH,
∵四边形ABCD和CDFE都是正方形,
∴DC=DF,∠DCG=∠DFH=∠FDC=90°,
∵∠CDG+∠CDH=∠CDH+∠FDH=90°,
∴∠CDG=∠FDH,
∴△CDG≌△FDH,
∴CG=FH,
∵BC=EF,
∴BG=EH.
(2)结论BG=EH仍然成立.
同理可证△CDG≌△FDH,
∴CG=FH,
∵BC=EF,
∴BG=EH.
点评:本题主要考查了正方形的性质和全等三角形的判定.通过全等三角形来得出简单的线段相等是解此类题的常用方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•德化县一模)友情提示:请同学们做完上面考题后,再认真检查一遍,估计一下你的得分情况.如果你全卷得分低于90分(及格线),则本题的得分将计入全卷总分,但计入后全卷总分最多不超过90分;如果你全卷总分已经达到或超过90分,则本题的得分不计入全卷总分.
(2012•德化县一模)友情提示:请同学们做完上面考题后,再认真检查一遍,估计一下你的得分情况.如果你全卷得分低于90分(及格线),则本题的得分将计入全卷总分,但计入后全卷总分最多不超过90分;如果你全卷总分已经达到或超过90分,则本题的得分不计入全卷总分.