Question

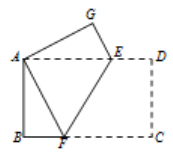
【题目】长方形具有四个内角均为直角，并且两组对边分别相等的特征.如图，把一张长方形纸片ABCD折叠，使点C与点A重合，折痕为EF.

（1）如果∠DEF＝130°，求∠BAF的度数；

（2）判断△ABF和△AGE是否全等吗？请说明理由.

Answer 1

【答案】（1）10°；（2）全等，理由见解析

【解析】试题分析：（1）在Rt△ABF中，求出∠AFB即可解决问题．

（2）结论：△ABF≌△AGE．只要证明，∠B=∠G，AB=AG，∠AFB=∠AEG，根据AAS即可判定．

解：（1）∵ABCD是长方形，

∴AD∥BC，AB=CD，

∴∠CFE=180°-∠DEF=50°，

由折叠知：∠AFE=∠CFE=50°，

∴∠AFB=180°-∠AFE-∠CFE=80°，

∵∠B=90°，

∴∠BAF=90°-∠AFB=10°.

（2）△ABF≌△AGE，理由如下：

则折叠知：AG=CD，∠G=∠D=90°，∠DEF=∠GEF=130°，

∴∠B=∠G，

∵AB=CD，∴AB=AG，

∵∠AEF=180°-∠DEF=50°，

∴∠AEG=∠GEF-∠AEF=80°，

∴∠AFB=∠AEG ，

∴△ABF≌△AGE（AAS）.