题目内容
 如图,已知抛物线l1:y=
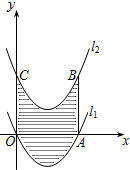
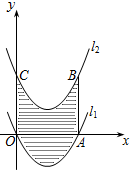
如图,已知抛物线l1:y= (x-2)2-2与x轴分别交于O、A两点,将抛物线l1向上平移得到l2,过点A作AB⊥x轴交抛物线l2于点B,如果由抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积为16,则抛物线l2的函数表达式为
(x-2)2-2与x轴分别交于O、A两点,将抛物线l1向上平移得到l2,过点A作AB⊥x轴交抛物线l2于点B,如果由抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积为16,则抛物线l2的函数表达式为
- A.y=
 (x-2)2+4
(x-2)2+4 - B.y=
 (x-2)2+3
(x-2)2+3 - C.y=
 (x-2)2+2
(x-2)2+2 - D.y=
 (x-2)2+1
(x-2)2+1
C
分析:根据题意可推知由抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积就是矩形ABCO的面积;然后再根据抛物线l1的解析式求得O、A两点的坐标,从而解得OA的长度;最后再由矩形的面积公式求得AB的长度,即l2是由抛物线l1向上平移多少个单位得到的.
解答: 解:连接BC,
解:连接BC,
∵l2是由抛物线l1向上平移得到的,
∴由抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积就是矩形ABCO的面积;
∵抛物线l1的解析式是y= (x-2)2-2,
(x-2)2-2,
∴抛物线l1与x轴分别交于O(0,0)、A(4,0)两点,
∴OA=4;
∴OA•AB=16,
∴AB=4;
∴l2是由抛物线l1向上平移4个单位得到的,
∴l2的解析式为:y= (x-2)2-2+4,即y=
(x-2)2-2+4,即y= (x-2)2+2.
(x-2)2+2.
故选C.
点评:主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养.要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.
分析:根据题意可推知由抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积就是矩形ABCO的面积;然后再根据抛物线l1的解析式求得O、A两点的坐标,从而解得OA的长度;最后再由矩形的面积公式求得AB的长度,即l2是由抛物线l1向上平移多少个单位得到的.
解答:
 解:连接BC,
解:连接BC,∵l2是由抛物线l1向上平移得到的,
∴由抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积就是矩形ABCO的面积;
∵抛物线l1的解析式是y=
 (x-2)2-2,
(x-2)2-2,∴抛物线l1与x轴分别交于O(0,0)、A(4,0)两点,
∴OA=4;
∴OA•AB=16,
∴AB=4;
∴l2是由抛物线l1向上平移4个单位得到的,
∴l2的解析式为:y=
 (x-2)2-2+4,即y=
(x-2)2-2+4,即y= (x-2)2+2.
(x-2)2+2.故选C.
点评:主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养.要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.

练习册系列答案
相关题目
 如图,已知抛物线l1:y=
如图,已知抛物线l1:y=| 1 |
| 2 |
A、y=
| ||
B、y=
| ||
C、y=
| ||
D、y=
|
 1关于x轴对称,以AC为对角线的平行四边形ABCD的第四个顶点为D.
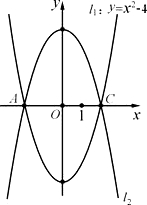
1关于x轴对称,以AC为对角线的平行四边形ABCD的第四个顶点为D. 28、如图,已知抛物线l1:y=x2-4的图象与x有交于A、C两点,
28、如图,已知抛物线l1:y=x2-4的图象与x有交于A、C两点, (2013•宝安区一模)如图,已知抛物线l1:y=-x2+2x与x轴分别交于A、O两点,顶点为M.将抛物线l1关于y轴对称到抛物线l2.则抛物线l2过点O,与x轴的另一个交点为B,顶点为N,连接AM、MN、NB,则四边形AMNB的面积( )
(2013•宝安区一模)如图,已知抛物线l1:y=-x2+2x与x轴分别交于A、O两点,顶点为M.将抛物线l1关于y轴对称到抛物线l2.则抛物线l2过点O,与x轴的另一个交点为B,顶点为N,连接AM、MN、NB,则四边形AMNB的面积( )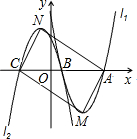 (2011•宝安区一模)如图,已知抛物线
(2011•宝安区一模)如图,已知抛物线