Question

（2013•宝安区一模）如图，已知抛物线l₁：y=-x²+2x与x轴分别交于A、O两点，顶点为M．将抛物线l₁关于y轴对称到抛物线l₂．则抛物线l₂过点O，与x轴的另一个交点为B，顶点为N，连接AM、MN、NB，则四边形AMNB的面积（　　）

A．3

B．6

C．8

D．10

Answer 1

分析：根据抛物线l₁的解析式求出顶点M，和x轴交点A的坐标，然后根据对称图形的知识可求出M、N的坐标，也可得到四边形NBAM是等腰梯形，求出四边形NBAM的面积即可．

解答：解：∵抛物线l₁的解析式为：y=-x²+2x=-（x-1）²+1，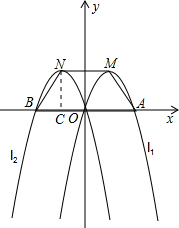
∴顶点坐标为：M（1，1），
当y=0时，-x²+2x=0，
解得：x=0或x=2，
则A坐标为（2，0），
∵l₂和l₁关于y轴对称，
∴AM=BN，N和M关于y轴对称，B和A关于y轴对称，
则N（-1，1），B（-2，0），
过N作NC⊥AB交AB与点C，
∵AM=BN，MN∥AB，
∴四边形NBAM是等腰梯形，
在等腰梯形NBAM中，
MN，1-（-1）=2，AB=2-（-2）=4，
NC=1，
∴S_{四边形NBAM}=

1

2

（MN+AB）•NC=3．
故选A．

点评：本题是二次函数的综合题型，其中涉及到的知识点有抛物线的顶点公式和等腰梯形的面积求法，根据对称图形得出N，B的坐标是解答本题的关键．