Question

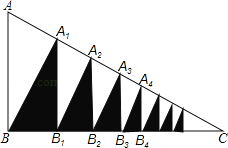
【题目】如图，在Rt△ABC中，AB＝3，BC＝4，∠ABC＝90°，过B作A1B⊥AC，过A1作A1B1⊥BC，得阴影Rt△A1B1B；再过B1作B1A2⊥AC，过A2作A2B2⊥BC，得阴影Rt△A2B2B1；…如此下去．请猜测这样得到的所有阴影三角形的面积之和为_____．

Answer 1

【答案】

【解析】

根据相似三角形的性质，相似三角形的面积比等于相似比的平方，那么阴影部分面积与空白部分面积之比为16：25，那么所有的阴影部分面积之和可求了．

解：∵在Rt△ABC中，AB＝3，BC＝4，∠ABC＝90°，

∴AC=，

∴，

∵∠ABC＝90°，A1B1⊥BC，

∴AB∥A1B1，∠A1B1B=90°，

∴∠ABA1=∠BA1B1，

∴△ABA1∽△BA1B1，

∴相似比为，

=16：25，

同理可得到其他三角形之间也是这个情况，

那么所有的阴影部分面积之和应等于＝3×4÷2×＝．

故答案为：．