Question

【题目】在y轴右侧且平行于y轴的直线l被反比例函数（）与函数（）所截，当直线l向右平移4个单位时，直线l被两函数图象所截得的线段扫过的面积为__________平方单位．

【答案】8

【解析】∵y轴右侧且平行于y轴的直线l被反比例函数y=（x＞0）与函数y=+2（x＞0）所截，∴设它们的交点为A，C，∴AC=2，∵直线l向右平移4个单位，∴CD=4，∴直线l被两函数图象所截得的线段扫过的面积为 2×4=8平方单位．故答案为8.

【题型】填空题
【结束】
14

【题目】函数的图象如右图所示，则结论：

①两函数图象的交点的坐标为； ②当时， ；

③当时， ； ④当逐渐增大时， 随着的增大而增大， 随着的增大而减小．

其中正确结论的序号是 ．

Answer 1

【答案】①③④

【解析】试题分析：反比例函数与一次函数的交点问题．运用一次函数和反比例函数的性质来解决的一道常见的数形结合的函数试题．一次函数和反比例函数的交点坐标就是一次函数与反比例函数组成的方程组的解．根据k＞0确定一次函数和反比例函数在第一象限的图象特征来确定其增减性；根据x=1时求出点B点C的坐标从而求出BC的值；当x=2时两个函数的函数值相等时根据图象求得x＞2时y1＞y2．

试题解析：①由一次函数与反比例函数的解析式，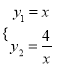

解得， ，

∴A（2，2），故①正确；

②由图象得x＞2时，y1＞y2；故②错误；

③当x=1时，B（1，3），C（1，1），∴BC=3，故③正确；

④一次函数是增函数，y随x的增大而增大，反比例函数k＞0，y随x的增大而减小．故④正确．

∴①③④正确．