题目内容
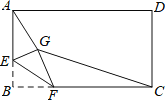
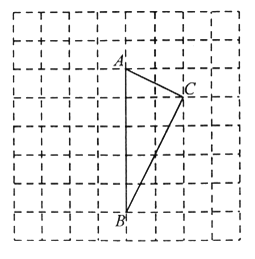
【题目】如图,在每个小正方形的边长为1的网格中,△ABC的顶点A,B,C均在格点上,
(I)△ABC是_____________三角形(填“锐角”、“直角”或“钝角”):
(Ⅱ)若P,Q分别为边AB,BC上的动点,当PC+PQ取得最小值时,在如图所示的网格中,用无刻度的直尺,画出线段PC,PQ,并简要说明点2的位置是如何找到的(不要求证明).
________________________________________________________________________________
【答案】直角; 取格点![]() ,连接
,连接![]() 并延长交BC于点Q
并延长交BC于点Q
【解析】
(I)根据勾股定理得到三边的长度,再根据三边的关系判断三角形的形状;
(Ⅱ)要求PC+PQ的最小值,只需作点C关于AB的对称点C’,并从C’向BC作垂线则与AB,BC分别交于点P,Q为所求.
(I)∵AC= ![]() ,BC=
,BC= ![]() ,AB=5,
,AB=5,
∴AC2+BC2=AB2,
∴△ABC是直角三角形.
(Ⅱ)
要求PC+PQ的最小值,只需作点C关于AB的对称点C’,并从C’向BC作垂线则与AB,BC分别交于点P,Q为所求.
作法:取格点C’,则C’为点C关于AB的对称点,由①可知,AC⊥BC,则只需过C’作AC的平行线,只需取格点P则AC∥C’P,延长C’P交AB,BC于点P,Q.
取格点![]() ,连接
,连接![]() 并延长交BC于点Q
并延长交BC于点Q


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某校为改善办学条件,计划购进![]() 两种规格的书架,经市场调查发现有线下和线上两种方式,具有情况如下表:
两种规格的书架,经市场调查发现有线下和线上两种方式,具有情况如下表:
规格 | 线下 | 线上 | ||
单价(元/个) | 运费(元/个) | 单价(元/个) | 运费(元/个) | |
A | 240 | 0 | 210 | 20 |
B | 300 | 0 | 250 | 30 |
(Ⅰ)如果在线下购买![]() 两种书架20个,共花费5520元,求
两种书架20个,共花费5520元,求![]() 两种书架各购买了多少个;
两种书架各购买了多少个;
(Ⅱ)如果在线上购买![]() 两种书架20个,共花费
两种书架20个,共花费![]() 元,设其中
元,设其中![]() 种书架购买
种书架购买![]() 个,求W关于
个,求W关于![]() 的函数关系式;
的函数关系式;
(Ⅲ)在(Ⅱ)的条件下,若购买![]() 种书架的数量不少于
种书架的数量不少于![]() 种书架的2倍,请求出花费最少的购买方案,并计算按照该购买方案线上比线下节约多少钱.
种书架的2倍,请求出花费最少的购买方案,并计算按照该购买方案线上比线下节约多少钱.