题目内容
已知抛物线y=ax2+bx+c的图象与x轴正半轴交于点A、B,点A在点B的左侧,与y轴负半轴交于点C,且OA=AB=OC=1,则该抛物线的顶点坐标为
(
,
)
| 3 |
| 2 |
| 1 |
| 8 |
(
,
)
.| 3 |
| 2 |
| 1 |
| 8 |
分析:根据OA=AB=OC=1知,点A(1,0),B(2,0)(0,1),然后利用待定系数法求得该抛物线的解析式,将抛物线解析式写为顶点式方程,易求该抛物线的顶点.
解答: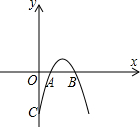 解:如图,∵OA=AB=OC=1,
解:如图,∵OA=AB=OC=1,
∴A(1,0),B(2,0),C(0,-1),
∴
,
解得,
,
∴该抛物线的解析式是:y=-
x2+
x-1=0,即y=
(x-
)x2+
,
∴该抛物线的顶点坐标为(
,
).
故答案是:(
,
).
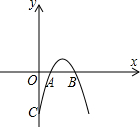 解:如图,∵OA=AB=OC=1,
解:如图,∵OA=AB=OC=1,∴A(1,0),B(2,0),C(0,-1),
∴
|
解得,
|
∴该抛物线的解析式是:y=-
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 8 |
∴该抛物线的顶点坐标为(
| 3 |
| 2 |
| 1 |
| 8 |
故答案是:(
| 3 |
| 2 |
| 1 |
| 8 |
点评:本题考查了抛物线与x轴的交点.解题的关键是根据已知条件求得点A、B、C的坐标.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 与x轴的另一个交点为E.
与x轴的另一个交点为E. 如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=
如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=