题目内容
【题目】等腰三角形ABC中,AB=AC,点D是AC上一点。点E在BD的延长线上,且AB=AE,AF平分∠CAE交DE于点F,连接CF
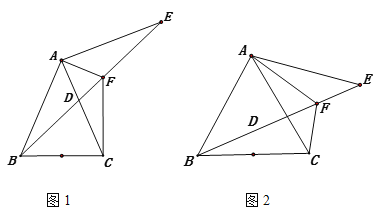
(1)如图1,找到与∠CFB相等的角,并证明
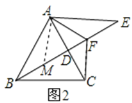
(2)如图2,如当∠ABC=60°,AF=m,EF=n时,求FB的长(用含m、n的式子表示)
【答案】(1)见解析;(2) m+n.
【解析】
(1)证△EAF≌△CAF,推出EF=CF,∠E=∠ACF,根据等腰三角形性质推出∠E=∠ABF,即可得出答案;
(2)在FB上截取BM=CF,连接AM,证△ABM≌△ACF,推出EF=FC=BM,AF=AM,推出△AMF是等边三角形,推出MF=AF,即可得出答案;
证明:(1)∠CFB=∠CAB,
∵AF平分∠CAE,
∴∠EAF=∠CAF,
∵AB=AC,AB=AE,
∴AE=AC,
在△ACF和△AEF中,
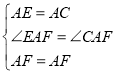 ,
,
∴△ACF≌△AEF(SAS),
∴∠E=∠ACF,
∵AB=AE,
∴∠E=∠ABE,
∴∠ABE=∠ACF,
∵∠ADB=∠CDF,
∴∠CFB=∠CAB;
(2)如图2,
∵△ACF≌△AEF,
∴EF=CF,∠E=∠ACF=∠ABM,
在FB上截取BM=CF,连接AM,
在△ABM和△ACF中,
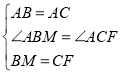 ,
,
∴△ABM≌△ACF(SAS),
∴AM=AF,∠BAM=∠CAF,
∵AB=AC,∠ABC=60°,
∴△ABC是等边三角形,
∴∠BAC=60°,
∴∠MAF=∠MAC+∠CAF=∠MAC+∠BAM=∠BAC=60°,
∵AM=AF,
∴△AMF为等边三角形,
∴AF=AM=MF,
∴AF+EF=BM+MF=FB,
∵AF=m,EF=n,
即FB=m+n.

【题目】某水果商店经销一种苹果,共有20筐,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如表:
与标准质量的差值(单位;千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)这20筐苹果中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,这20筐苹果总计超过或不足多少千克?
(3)若苹果每千克售价![]() 元,则出售这20筐苹果可卖多少元?
元,则出售这20筐苹果可卖多少元?
【题目】某超市在“十一”长假期间对顾客实行优惠,规定如下:
一次性购物金额 | 优惠办法 |
不超过100元 | 不予优惠 |
超过100元但不超过500元 | 超过100元部分给予九折优惠 |
超过500元 | 超过500元部分给予八折优惠 |
(1)小明的爷爷一次性购200元的保健食品,他实际付款_____元;小明妈妈一次性购300元的衣服,她实际付款_____元;如果他们两人合作付款,则能少付_____元;
(2)小芳奶奶在该超市一次性购物x元生活用品,当x大于或等于500时,她实际付款_____元;(用含x的式子表示,写最简结果)
(3)如果小芳奶奶两次购物货款合计900元,第一次购物的货款为a元(![]() ),两次购物小芳奶奶实际付款多少元?(用含a的式子表示)
),两次购物小芳奶奶实际付款多少元?(用含a的式子表示)