题目内容
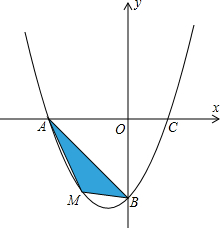 在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点.
在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点.(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S、求S关于m的函数关系式,并求出S的最大值.
(3)若点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
分析:(1)由待定系数法将A(-4,0),B(0,-4),C(2,0)三个点的坐标代入y=ax2+bx+c,联立求解即可;
(2)过M作x轴的垂线,设垂足为D.设点M的坐标为(m,n),即可用含m的代数式表示MD、OD的长,分别求出△AMD、梯形MDOB、△AOB的面积,那么△AMD、梯形MDOB的面积和减去△AOB的面积即为△AMB的面积,由此可得关于S、m的函数关系式,根据函数的性质即可求得S的最大值.
(3)解决此题需要充分利用平行四边形的性质求解.设P(x,
x2+x-4),
①如图1,当OB为边时,根据平行四边形的性质知PQ∥OB,则Q(x,-x).由PQ=OB即可求出结论;
②如图2,当OB为对角线时,那么P、Q的横坐标互为相反数(若P的横坐标为x,则Q的横坐标为-x),即Q(-x,x).由P、O的纵坐标差的绝对值等于Q、B纵坐标差的绝对值,得
x2+x-4=-4-x,求出x的值即可.
(2)过M作x轴的垂线,设垂足为D.设点M的坐标为(m,n),即可用含m的代数式表示MD、OD的长,分别求出△AMD、梯形MDOB、△AOB的面积,那么△AMD、梯形MDOB的面积和减去△AOB的面积即为△AMB的面积,由此可得关于S、m的函数关系式,根据函数的性质即可求得S的最大值.
(3)解决此题需要充分利用平行四边形的性质求解.设P(x,
| 1 |
| 2 |
①如图1,当OB为边时,根据平行四边形的性质知PQ∥OB,则Q(x,-x).由PQ=OB即可求出结论;
②如图2,当OB为对角线时,那么P、Q的横坐标互为相反数(若P的横坐标为x,则Q的横坐标为-x),即Q(-x,x).由P、O的纵坐标差的绝对值等于Q、B纵坐标差的绝对值,得
| 1 |
| 2 |
解答:解:(1)设抛物线的解析式为y=a(x+4)(x-2),
把B(0,-4)代入得,-4=a×(0+4)(0-2),解得a=
,
∴抛物线的解析式为:y=
(x+4)(x-2),即y=
x2+x-4;
(2)过点M作MD⊥x轴于点D,设M点的坐标为(m,n),
则AD=m+4,MD=-n,n=
m2+m-4,
∴S=S△AMD+S梯形DMBO-S△ABO
=
(m+4)(-n)+
(-n+4)(-m)-
×4×4
=-2n-2m-8
=-2×(
m2+m-4)-2m-8
=-m2-4m
=-(m+2)2+4(-4<m<0);
∴S最大值=4.
(3)设P(x,
x2+x-4).
①如图1,当OB为边时,根据平行四边形的性质知PQ∥OB,
∴Q的横坐标等于P的横坐标,
又∵直线的解析式为y=-x,
则Q(x,-x).
由PQ=OB,得|-x-(
x2+x-4)|=4,解得x=0,-4,-2±2
.x=0不合题意,舍去.由此可得Q(-4,4)或(-2+2
,2-2
)或(-2-2
,2+2
);
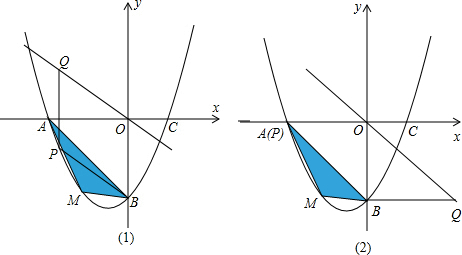
②如图2,当BO为对角线时,知A与P应该重合,OP=4.四边形PBQO为平行四边形则BQ=OP=4,Q横坐标为4,代入y=-x得出Q为(4,-4).
故满足题意的Q点的坐标有四个,分别是(-4,4),(4,-4),(-2+2
,2-2
),(-2-2
,2+2
).
把B(0,-4)代入得,-4=a×(0+4)(0-2),解得a=
| 1 |
| 2 |
∴抛物线的解析式为:y=
| 1 |
| 2 |
| 1 |
| 2 |
(2)过点M作MD⊥x轴于点D,设M点的坐标为(m,n),

则AD=m+4,MD=-n,n=
| 1 |
| 2 |
∴S=S△AMD+S梯形DMBO-S△ABO
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=-2n-2m-8
=-2×(
| 1 |
| 2 |
=-m2-4m
=-(m+2)2+4(-4<m<0);
∴S最大值=4.
(3)设P(x,
| 1 |
| 2 |
①如图1,当OB为边时,根据平行四边形的性质知PQ∥OB,
∴Q的横坐标等于P的横坐标,
又∵直线的解析式为y=-x,
则Q(x,-x).
由PQ=OB,得|-x-(
| 1 |
| 2 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |

②如图2,当BO为对角线时,知A与P应该重合,OP=4.四边形PBQO为平行四边形则BQ=OP=4,Q横坐标为4,代入y=-x得出Q为(4,-4).
故满足题意的Q点的坐标有四个,分别是(-4,4),(4,-4),(-2+2
| 5 |
| 5 |
| 5 |
| 5 |
点评:此题主要考查了二次函数解析式的确定、图形面积的求法、二次函数最值的应用以及平行四边形的判定和性质;此题的难点在于(3)题,需要熟练掌握平行四边形的性质,并且要考虑到各种情况才能做到不漏解.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=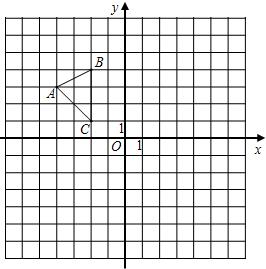 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.