Question

如图，点E是正方形ABCD的边BC上的一点，将正方形进行翻折，使点A与点E重合．
（1）在图中作出折痕MN（要求尺规作图并保留作图痕迹，不要求写作法）；
（2）设M在CD上，N在AB上．若tan∠AEN=

1

3

，DC+CE=10，求△NAE的面积．

Answer 1

（1）如图所示：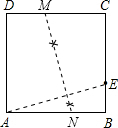

（2）由折叠可知：MN为AE的垂直平分线，
∴AN=EN，
∴∠EAN=∠AEN（等角对等边），
∴tan∠AEN=tan∠EAN=

1

3

，
∴设BE=a，AB=3a，则CE=2a，
∵DC+CE=10，
∴3a+2a=10，
∴a=2，
∴BE=2，AB=6，CE=4，
∵AE=

4+36

=2

10

，
又∵

NG

AG

=

1

3

，
∴NG=

10

3

，
∴AN=

( 10 )2+( 10 3 )2

=

10

3

，
∴AN=NE=

10

3

，
∴S_△ANE=

1

2

×

10

3

×2=

10

3

．