题目内容
（2013•浦东新区一模）如图，已知在△ABC中，边BC=6，高AD=3，正方形EFGH的顶点F、G在边BC上，顶点E、H分别在边AB和AC上，那么这个正方形的边长等于（ ）分析：利用正方形的性质可知EH∥BC，再利用平行线分线段成比例定理的推论可得△AHE∽△ACB，利用相似三角形的性质可得比例线段，利用比例线段可求正方形的边长
解答：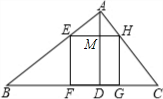
解：∵四边形EFMN是正方形，
∴EH∥BC，EH=EF，
∴△AEH∽△ABC，
又∵AD⊥BC，
∴AD⊥BC，EH=EF=MD，
∴
=
，
设EH=x，则AM=3-x，
∴
=
，
解得：x=2，
∴EH=2．
答：这个正方形的边长为2．
故选C．
解：∵四边形EFMN是正方形，∴EH∥BC，EH=EF，
∴△AEH∽△ABC，
又∵AD⊥BC，
∴AD⊥BC，EH=EF=MD，
∴
| AM |
| AD |
| EH |
| BC |
设EH=x，则AM=3-x，
∴
| 3-x |
| 3 |
| x |
| 6 |
解得：x=2，
∴EH=2．
答：这个正方形的边长为2．
故选C．
点评：本题考查了相似三角形的判定和性质、正方形的性质和平行线分线段成比例定理，是各地中考考查相似三角形常见题型．
练习册系列答案
相关题目