题目内容
【题目】如图，一艘轮船位于灯塔P的北偏东60°方向，与灯塔P的距离为30海里的A处，轮船沿正南方向航行一段时间后，到达位于灯塔P的南偏东30°方向上的B处，则此时轮船所在位置B处与灯塔P之间的距离为（ ）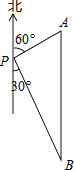
A.60海里
B.45海里
C.20 
海里
D.30 海里
【答案】D
【解析】解：由题意可得：∠B=30°，AP=30海里，∠APB=90°，
故AB=2AP=60（海里），
则此时轮船所在位置B处与灯塔P之间的距离为：BP= 
=30 
（海里）
所以答案是：D．
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2，以及对关于方向角问题的理解，了解指北或指南方向线与目标方向 线所成的小于90°的水平角，叫做方向角．
轻松暑假总复习系列答案
【题目】近年来，我国很多地区持续出现雾霾天气．某社区为了调查本社区居民对雾霾天气主要成因的认识情况，随机对该社区部分居民进行了问卷调查，要求居民从五个主要成因中只选择其中的一项，被调查居民都按要求填写了问卷．社区对调查结果进行了整理，绘制了如下不完整的统计图表．被调查居民选择各选项人数统计表
雾霾天气的主要成因 | 频数（人数） |
A大气气压低，空气不流动 | m |
B地面灰尘大，空气湿度低 | 40 |
C汽车尾气排放 | n |
D工厂造成的污染 | 120 |
E其他 | 60 |
请根据图表中提供的信息解答下列问题：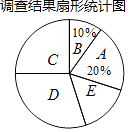
（1）填空：m= ， n= ， 扇形统计图中C选项所占的百分比为 ．
（2）若该社区居民约有6 000人，请估计其中会选择D选项的居民人数．
（3）对于“雾霾”这个环境问题，请你用简短的语言发出倡议．
【题目】抗震救灾中，某县粮食局为了保证库存粮食的安全，决定将甲、乙两个仓库的粮食，全部转移到具有较强抗震功能的A、B两仓库．已知甲库有粮食100吨，乙库有粮食80吨，而A库的容量为70吨，B库的容量为110吨．从甲、乙两库到A、B两库的路程和运费如下表：（表中“元/吨千米”表示每吨粮食运送1千米所需人民币）
路程（千米） | 运费（元/吨千米） | |||
甲库 | 乙库 | 甲库 | 乙库 | |
A库 | 20 | 15 | 12 | 12 |
B库 | 25 | 20 | 10 | 8 |
（1）若甲库运往A库粮食x吨，请写出将粮食运往A、B两库的总运费y（元）与x（吨）的函数关系式；
（2）当甲、乙两库各运往A、B两库多少吨粮食时，总运费最省，最省的总运费是多少？
