题目内容
9、方程y2=x2+2006的正整数解的个数是
0
．分析：运用平方差分解方程，然后进行奇偶性分析，得出分解两式的奇偶情况，从而可确定结果．
解答：解：∵求y2=x2+2006的正整数解，
y2-x2=2006
显然x、y＞0，y＞xy2-x2=（x+y）（y-x）=2006=2×1003因（x+y）、（y-x）奇偶性相同，又因2006含偶因数．所以（y+x）、（y-x）必同偶．而y2-x2只能分解成一个奇数和一个偶数，所以找不到这样的一组数据．
故答案为：0
y2-x2=2006
显然x、y＞0，y＞xy2-x2=（x+y）（y-x）=2006=2×1003因（x+y）、（y-x）奇偶性相同，又因2006含偶因数．所以（y+x）、（y-x）必同偶．而y2-x2只能分解成一个奇数和一个偶数，所以找不到这样的一组数据．
故答案为：0
点评：此题考查了平方差公式以及两数相乘积的情况，难度不大，应细心分析．
练习册系列答案
相关题目
用换元法解方程x2+3x-
=8，若设x2+3x=y，则原方程可化为（ ）
| 20 |
| x2+3x |
| A、20y2+8y-1=0 |
| B、8y2-20y+1=0 |
| C、y2+8y-20=0 |
| D、y2-8y-20=0 |
用换元法解方程x2+2x-
=8，若设x2+2x=y，则原方程可化为（ ）
| 20 |
| x2+2x |
| A、y2-8y-20=0 |
| B、8y2-20y+1=0 |
| C、y2+8y-20=0 |
| D、20y2+8y-1=0 |
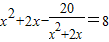，若设x2+2x=y，则原方程可化为（ ）
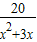=8，若设x2+3x=y，则原方程可化为（ ）