题目内容
【题目】已知二次函数y=x2-4x+3.
(1)该函数与x轴的交点坐标 ;
(2)在平面直角坐标系中,用描点法画出该二次函数的图象;
x | … | 0 | 1 | 2 | 3 | 4 | … |
y | … | 3 | 0 | -1 | 0 | 3 | … |
(3)根据图象回答:
①当自变量x的取值范围满足什么条件时,y<0?
②当0≤x<3时,y的取值范围是多少?
【答案】(1) (1,0),(3,0);(2)画图见解析;(3)①当1<x<3时,y<0;②当0≤x<3时,y的取值范围是-1≤y≤3.
【解析】试题分析:(1)要求二次函数与x轴的交点坐标即看表格里面y=0时对应的点的坐标即可求得;(2)画出数轴,在数轴上依次描出点的坐标,将点连接起来画出二次函数图象即可;(3)①确定二次函数当y小于0时对应的图象,再根据图象读出x对应的范围即可;②确定0≤x<3对应的图象,通过图像可得出y对应的范围.
试题解析:
(1) (1,0),(3,0);
(2)如图所示:
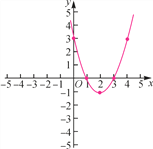
(3)①当1<x<3时,y<0;
②当0≤x<3时,y的取值范围是-1≤y≤3.

练习册系列答案
相关题目
【题目】(7分)某产品每件的成本10元,试销阶段每件产品的销售价![]() (元)与产品的日销售量
(元)与产品的日销售量![]() (件)之间的关系如下表:
(件)之间的关系如下表:
| 15 | 20 | 30 | … |
| 25 | 20 | 10 | … |
且日销售量![]() (件)是销售价
(件)是销售价![]() (元)的一次函数.
(元)的一次函数.
(1)求出日销售量![]() (件)与销售价
(件)与销售价![]() (元)的函数关系式;
(元)的函数关系式;
(2)要使每日的销售利润最大,每件产品的销售价应定为多少元?此时最大销售利润是多少?




