Question

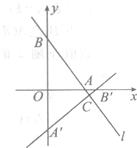在平面直角坐标系中，直线L：y=-

4

3

+4分别交x轴、y轴于点A、B，在X轴的正半轴上截取OB′=OB，在Y轴的负半轴上截取OA′=OA，如图所示．
（1）求直线A′B′的解析式．
（2）若直线．A′B′与直线L相交于点C，求C点的坐标．

Answer 1

分析：（1）根据题意即可求出OA，OB的长度，然后根据OB′=OB，OA′=OA，再根据A′，B′点的位置即可推出A′，B′两点的坐标，设直线A′B′的解析式为y=kx+b，把A′，B′两点的坐标代入解析式，即可求出k，b的值，即推出直线A′B′的解析式；
（2）根据（1）所推出的结论，结合直线AB的解析式，组成一个二元一次方程组，通过解方程求出x，y的值，即为两直线交点C的横纵坐标．

解答：解：（1）∵直线L：y=-

4

3

+4，
∴y=0，得x=3，即OA=3，
∵OA′=OA，
∴OA′=OA=3，
∵A′点在y轴的负半轴上，
∴点A′的坐标（0，-3），
∴当x=0，得y=4，即OB=4，
∵OB′=OB，
∴OB′=OB=4，
∵B′点在x轴的正半轴上，
∴点B′的坐标（4，0），
设直线A′B′的解析式为y=kx+b，
∵A′的坐标（0，-3），点B′的坐标（4，0）
∴b=-3，k=

3

4

，
∴直线A′B′的解析式为y=

3

4

x-3，

（2）∵A′B′与直线L相交于点C，根据题意得方程组：

y= - 4 3 x+4 y= 3 4 x-3

，
解方程组得：

x= 84 25 y=- 12 25

，
∴交点C的坐标（

84

25

，-

12

25

）．

点评：本题主要考查用待定系数法求一次函数解析式，解二元一次方程组，关键在于运用数形结合的思想求出A′，B′两点的坐标，根据题意正确的列出方程组，认真的解方程组．