题目内容

如果四边形ABCD是⊙O的内接四边形，那么下列结论不正确的是（　　）
分析：先根据题意画出图形，在根据圆内接四边形的性质对各选项进行逐一分析即可．
解答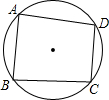：解：如图所示：
∵四边形ABCD是⊙O的内接四边形，
∴∠A+∠C=180°，∠B+∠D=180°，故B、C正确；
∴∠A+∠C+∠B＞180°，∠D＜180°，
∴∠A+∠B+∠C＞∠D，故D选项正确，
∵∠A与∠B不是相对的角，
∴∠A与∠B的和不能确定，故A选项错误．
故选A．
点评：本题考查的是圆内接四边形的性质，即圆内接四边形的对角互补．
练习册系列答案
相关题目
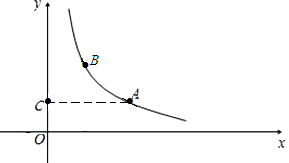精英家教网如图，反比例函数y=
kx
（x＞0）上有两点A（4，1）、B（a，b）：（0＜a＜4），过点A作AC⊥y轴于点C，
（1）求此反比例函数的解析式；
（2）在坐标平面内有一点D，使四边形ABCD是菱形，求出B、D两点的坐标；
（3）如果四边形ABCD是平行四边形，且面积为12，求出此平行四边形对角线可达的最大长度．
操作1：如图1，一三角形纸片ABC，分别取AB、AC的中点D、E，连接DE，沿DE将纸片剪开，并将其中的△ADE纸片绕点E旋转180°后可拼合（无重叠无缝隙）成平行四边形纸片BCFD．
操作2：如图2，一平行四边形纸片ABCD，E、F、G、H分别是AB、BC、CD、AD边的中点，沿EF剪开并将其中的△BFE纸片绕点E旋转180°到△AF1E位置；沿HG剪开并将其中的△DGH纸片绕点H旋转180°到△AG1H位置；沿FG剪开并将△CFG纸片放置于△AF1G1的位置，此时四张纸片恰好拼合（无重叠无缝隙）成四边形FF1G1G．则四边形FF1G1G的形状是
 
．
精英家教网
操作、思考并探究：
（1）如图3，如果四边形ABCD是任意四边形（不是梯形或平行四边形）的纸片，E、F、G、H分别是AB、BC、CD、AD的中点．依次沿EF、FG、GH、HE剪开得到四边形纸片EFGH．请判断四边形纸片EFGH的形状，并说明理由．
（2）你能将上述四边形纸片ABCD经过恰当地剪切后拼合（无重叠无缝隙）成一个平行四边形纸片？请在图4上画出对应的示意图．
精英家教网
（3）如图5，E、F、G、H分别是四边形ABCD各边的中点，若△AEH、△BEF、△CFG、△DGH的面积分别为S1、S2、S3、S4，且S1=2，S3=5，则四边形ABCD是面积是
 
．（不要求说明理由）
（1）如图，如果四边形ABCD是任意四边形（不是梯形或平行四边形）的纸片，E、F、G、H分别是AB、BC、CD、AD的中点．依次沿EF、FG、GH、HE剪开得到四边形纸片EFGH．请判断四边形纸片EFGH的形状，并说明理由．
精英家教网
（2）你能将上述四边形纸片ABCD经过恰当地剪切后拼合（无重叠无缝隙）成一个平行四边形纸片吗？请在图上画出对应的示意图．
（3）如图，E，F，G，H分别是四边形ABCD各边的中点，若△AEH，△BEF，△CFG，△DGH的面积分别为S1，S2，S3，S4，且S1=2，S3=5，则四边形ABCD是面积是
 
．（不要求说明理由）
5、下面给出的四个命题中，是假命题的是（　　）
5、下列命题中真命题是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网