题目内容
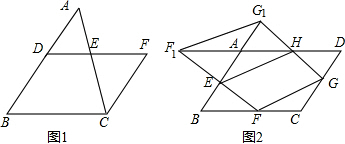
操作1:如图1,一三角形纸片ABC,分别取AB、AC的中点D、E,连接DE,沿DE将纸片剪开,并将其中的△ADE纸片绕点E旋转180°后可拼合(无重叠无缝隙)成平行四边形纸片BCFD.操作2:如图2,一平行四边形纸片ABCD,E、F、G、H分别是AB、BC、CD、AD边的中点,沿EF剪开并将其中的△BFE纸片绕点E旋转180°到△AF1E位置;沿HG剪开并将其中的△DGH纸片绕点H旋转180°到△AG1H位置;沿FG剪开并将△CFG纸片放置于△AF1G1的位置,此时四张纸片恰好拼合(无重叠无缝隙)成四边形FF1G1G.则四边形FF1G1G的形状是
操作、思考并探究:
(1)如图3,如果四边形ABCD是任意四边形(不是梯形或平行四边形)的纸片,E、F、G、H分别是AB、BC、CD、AD的中点.依次沿EF、FG、GH、HE剪开得到四边形纸片EFGH.请判断四边形纸片EFGH的形状,并说明理由.
(2)你能将上述四边形纸片ABCD经过恰当地剪切后拼合(无重叠无缝隙)成一个平行四边形纸片?请在图4上画出对应的示意图.

(3)如图5,E、F、G、H分别是四边形ABCD各边的中点,若△AEH、△BEF、△CFG、△DGH的面积分别为S1、S2、S3、S4,且S1=2,S3=5,则四边形ABCD是面积是
分析:操作2:根据一组对边平行且相等的四边形是平行四边形进行分析判断;
(1)根据一组对边平行且相等的四边形是平行四边形进行分析判断;
(2)依照操作2进行画图;
(3)根据三角形的中位线定理和相似三角形的性质求解.
(1)根据一组对边平行且相等的四边形是平行四边形进行分析判断;
(2)依照操作2进行画图;
(3)根据三角形的中位线定理和相似三角形的性质求解.
解答:
解:操作2:连接BD.
根据三角形的中位线定理,得
EH∥BD,EH=
BD,FG∥BD,FG=
BD,
根据旋转的性质,得F1G1∥EH,F1G1=EH.
所以F1G1∥FG,F1G1=FG,
所以四边形FF1G1G的形状是平行四边形.

(1)连接BD.
根据三角形的中位线定理,得
EH∥BD,EH=
BD,FG∥BD,FG=
BD,
则EH∥FG,EH=FG,
则四边形纸片EFGH的形状是平行四边形.
(2)见上述操作2;
(3)28.

解:操作2:连接BD.
根据三角形的中位线定理,得
EH∥BD,EH=
| 1 |
| 2 |
| 1 |
| 2 |
根据旋转的性质,得F1G1∥EH,F1G1=EH.
所以F1G1∥FG,F1G1=FG,
所以四边形FF1G1G的形状是平行四边形.

(1)连接BD.
根据三角形的中位线定理,得
EH∥BD,EH=
| 1 |
| 2 |
| 1 |
| 2 |
则EH∥FG,EH=FG,
则四边形纸片EFGH的形状是平行四边形.
(2)见上述操作2;
(3)28.
点评:此题综合考查了三角形的中位线定理、旋转的性质以及相似三角形的性质.

练习册系列答案
相关题目



 15、如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;…,根据以上操作,若要得到2011个小正方形,则需要操作的次数是
15、如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;…,根据以上操作,若要得到2011个小正方形,则需要操作的次数是
 (2011•沙坪坝区模拟)如图,将一张正三角形纸片剪成四个小正三角形,得到4个小正三角形,称为第一次操作;然后,将其中的一个正三角形再剪成四个小正三角形,共得到7个小正三角形,称为第二次操作;再将其中的一个正三角形再剪成四个小正三角形,共得到10个小正三角形,称为第三次操作;…,根据以上操作,若要得到2011个小正三角形,则需要操作的次数是( )
(2011•沙坪坝区模拟)如图,将一张正三角形纸片剪成四个小正三角形,得到4个小正三角形,称为第一次操作;然后,将其中的一个正三角形再剪成四个小正三角形,共得到7个小正三角形,称为第二次操作;再将其中的一个正三角形再剪成四个小正三角形,共得到10个小正三角形,称为第三次操作;…,根据以上操作,若要得到2011个小正三角形,则需要操作的次数是( ) (2013•吴中区二模)如图,将一张正三角形纸片剪成四个小正三角形,得到4个小正三角形,称为第一次操作;然后,将其中的一个正三角形再剪成四个小正三角形,共得到7个小正三角形,称为第二次操作;再将其中的一个正三角形再剪成四个小正三角形,共得到10个小正三角形,称为第三次操作;…,根据以上操作,若要得到2014个小正三角形,则需要操作的次数是( )次.
(2013•吴中区二模)如图,将一张正三角形纸片剪成四个小正三角形,得到4个小正三角形,称为第一次操作;然后,将其中的一个正三角形再剪成四个小正三角形,共得到7个小正三角形,称为第二次操作;再将其中的一个正三角形再剪成四个小正三角形,共得到10个小正三角形,称为第三次操作;…,根据以上操作,若要得到2014个小正三角形,则需要操作的次数是( )次.